题目内容

函数f（x）=ex+x2-2在区间（-2，1）内零点的个数为
 
．
考点：函数的零点与方程根的关系,函数零点的判定定理
专题：作图题,数形结合法
分析：函数f（x）=ex+x2-2在区间（-2，1）内零点的个数，即函数y=ex与函数y=2-x2在区间（-2，1）内交点个数，作出2个函数的图象，发现其交点的个数，即可得答案．
解答： 解：根据题意，函数f（x）=ex+x2-2在区间（-2，1）内零点的个数，
即函数y=ex与函数y=2-x2在区间（-2，1）内交点个数，
作图可得，这两个函数有2个交点，
即函数f（x）=ex+x2-2在区间（-2，1）内有2个零点，
故答案为：2．
点评：本题考查函数零点的判断方法，关键是正确画出2个函数的图象．
练习册系列答案
相关题目
若函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x+b，则f（-1）=
 
．
(-1+i)(2+i)
i3
=
 
．
关于函数f（x）=4sin（2x+
π
3
）（x∈R），有如下说法：
①y=f（x）的图象可由y=4sin2x的图象上所有的点向左平移
π
3
个单位而得到；
②y=f（x）的图象可由y=4sin（x+
π
3
）图象上所有点的横坐标伸长到原来的2倍  （纵坐标不变）而得到；
③y=f（x）的图象关于点（-
π
6
，0）对称；
④y=f（x）的图象关于直线x=
π
3
对称
其中，正确的说法是
 
（列出所有你认为正确的说法）
给出下列四个结论：
①若角的集合A={α|α=
kπ
2
+
π
4
，k∈Z}，B={β|β=kπ±
π
4
，k∈Z}，则A=B；
②sin
5π
7
＜cos
2π
7
＜tan
2π
7
；
③[kπ-
π
12
，kπ+
5π
12
]k∈Z是函数y=sin（
π
3
-2x）的单调递减区间；
④函数y=|tanx|的周期和对称轴方程分别为π，x=
kπ
2
（k∈Z）；
其中正确结论的序号是
 
．（请写出所有正确结论的序号）．
关于函数f（x）=cos2x-2
3
sinxcosx，下列命题：
①若存在x1，x2有x1-x2=π时，f（x1）=f（x2）成立；
②f（x）在区间[-
π
6
，
π
3
]上是单调递增；
③函数f（x）的图象关于点（
π
12
，0）成中心对称图象；
④将函数f（x）的图象向右平移
5π
12
个单位后将与y=2sin2x的图象重合．
其中正确的命题序号
 
（注：把你认为正确的序号都填上）
函数f（x）=sinx+cosx，在各项均为正数的数列{an}中对任意的n∈N*都有f（an+x）=f（an-x）成立，则数列{an}的通项公式可以为（写一个你认为正确的）
 
．
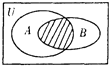
设全集U=R，A={x|x（x+2）＜0，B={x|x＜-1}，则图中阴影部分表示的集合为（　　）
A、{x|-2＜x＜0}
B、{x|-2＜x＜-1}
C、{x|x＞0}
D、{x|x＜-1}
非零向量
a
，
b
满足|
a
|=|
b
|=|
a
+
b
|，则
a
与
b
的夹角为（　　）
A、
π
3
B、
2π
3
C、
π
6
D、
5π
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网