题目内容
实数a,b,c,d满足(b+a2-3a)2+(c+d+2)2=0,则(a-c)2+(b+d)2的最小值是 .
考点:余弦定理
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:由平方数非负,得到:b+a2-3a=0,且c+d+2=0,由于(a-c)2+(b+d)2的几何意义:两点A(a,b)、B(c,-d)的距离的平方,则为求抛物线y=3x-x2上点A和直线x-y+2=0上点B的距离的最小值,先判断直线和抛物线相离,可设直线y=x+t与抛物线相切,由联立抛物线方程,运用判别式为0,求出t,再由两直线的距离公式,即可得到最小值,进而得到答案.
解答:
解:实数a,b,c,d满足(b+a2-3a)2+(c+d+2)2=0,
则有b+a2-3a=0,且c+d+2=0,
由于(a-c)2+(b+d)2的几何意义:两点A(a,b)、B(c,-d)的距离的平方,
则为求抛物线y=3x-x2上点A和直线x-y+2=0上点B的距离的最小值,
由于联立方程x-y+2=0和y=3x-x2上,消去y,得到x2-2x+2=0,方程无实数解,
故直线和抛物线相离,可设直线y=x+t与抛物线相切,
则联立抛物线方程,消去y,得,x2-2x+t=0,由判别式为0,即有4-4t=0,
即t=1,则切线为:y=x+1,
由于两直线y=x+2与直线y=x+1的距离为d=
=
,
即有抛物线y=3x-x2上点A和直线x-y+2=0上点B的距离的最小值为
,
则有(a-c)2+(b+d)2的最小值为
.
故答案为:
.
则有b+a2-3a=0,且c+d+2=0,
由于(a-c)2+(b+d)2的几何意义:两点A(a,b)、B(c,-d)的距离的平方,
则为求抛物线y=3x-x2上点A和直线x-y+2=0上点B的距离的最小值,
由于联立方程x-y+2=0和y=3x-x2上,消去y,得到x2-2x+2=0,方程无实数解,
故直线和抛物线相离,可设直线y=x+t与抛物线相切,
则联立抛物线方程,消去y,得,x2-2x+t=0,由判别式为0,即有4-4t=0,
即t=1,则切线为:y=x+1,
由于两直线y=x+2与直线y=x+1的距离为d=
| |2-1| | ||
|
| ||
| 2 |
即有抛物线y=3x-x2上点A和直线x-y+2=0上点B的距离的最小值为
| ||
| 2 |
则有(a-c)2+(b+d)2的最小值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查直线与抛物线的位置关系,考查两点距离的最值问题,注意运用切线知识,转化为直线间的距离,考查运算能力,属于中档题和易错题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 在正方体ABCD-A′B′C′D′中,P为棱AA′上一动点,Q为底面ABCD上一动点,M是PQ的中点,若点P,Q都运动时,点M构成的点集是一个空间几何体,则这个几何体是( )
在正方体ABCD-A′B′C′D′中,P为棱AA′上一动点,Q为底面ABCD上一动点,M是PQ的中点,若点P,Q都运动时,点M构成的点集是一个空间几何体,则这个几何体是( )| A、棱柱 | B、棱台 |
| C、棱锥 | D、球的一部分 |
方程|x|+|y|=1的曲线的周长及其所围成的区域的面积分别为( )
A、2
| ||
B、4
| ||
C、6
| ||
| D、8,4 |
定义在R上的偶函数f(x),函数f(x)在[0,+∞)上是减函数,则有( )
| A、f(3)<f(-2)<f(1) |
| B、f(1)<f(-2)<f(3) |
| C、f(-2)<f(1)<f(3) |
| D、f(3)<f(1)<f(-2) |
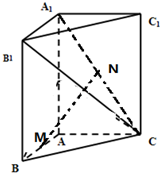 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.