题目内容
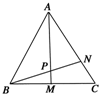如图所示，在△ABC中，点M是BC的中点，设| AB |
| a |
| AC |
| b |
（1）λ的值；
（2）用
| a |
| b |
| AP |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）由点M是BC的中点，利用向量平行四边形法则可得：
=
（
+
），因此
=
+
，由B、P、N三点共线，利用向量共线定理可得
=k
+（1-k）
=k
+
（1-k）
，再利用共面向量基本定理即可得出．
（2）利用（1）即可得出．
| AM |
| 1 |
| 2 |
| AB |
| AC |
| AP |
| λ |
| 2 |
| AB |
| λ |
| 2 |
| AC |
| AP |
| AB |
| AN |
| AB |
| 2 |
| 3 |
| AC |
（2）利用（1）即可得出．
解答：
解：（1）∵∴
=
（
+
），
∴
=
+
∵B、P、N三点共线，
∴
=k
+（1-k）
=k
+
（1-k）
，
∴
=k，
=
（1-k）
∴λ=
．
（2）由（1）可得
=
+
=
+
，
| AM |
| 1 |
| 2 |
| AB |
| AC |
∴
| AP |
| λ |
| 2 |
| AB |
| λ |
| 2 |
| AC |
∵B、P、N三点共线，
∴
| AP |
| AB |
| AN |
| AB |
| 2 |
| 3 |
| AC |
∴
| λ |
| 2 |
| λ |
| 2 |
| 2 |
| 3 |
∴λ=
| 4 |
| 5 |
（2）由（1）可得
| AP |
| λ |
| 2 |
| AB |
| λ |
| 2 |
| AC |
| 2 |
| 5 |
| a |
| 2 |
| 5 |
| b |
点评：本题考查了向量平行四边形法则、向量共线定理、共面向量基本定理，考查了推理能力和计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知ab＞0，且
+
≥m恒成立，则m的取值范围是（ ）
| b |
| a |
| a |
| b |
| A、{2} |
| B、[2，+∞） |
| C、（-∞，2] |
| D、[-2，+∞） |