题目内容

7．已知直线y=x-2与圆x2+y2=4交于两点M和N，O是坐标原点，则$\overrightarrow{OM}$$•\overrightarrow{ON}$=0．

分析 联立直线和圆的方程得到点M和点N的坐标，然后求解$\overrightarrow{OM}•\overrightarrow{ON}$即可．

解答 解：联立$\left\{\begin{array}{l}{y=x-2}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$，
则$\overrightarrow{OM}=（0，-2）$，$\overrightarrow{ON}=（2，0）$
所以$\overrightarrow{OM}•\overrightarrow{ON}$=0×2+（-2×0）=0，
故答案为：0．

点评 本题主要考察直线和圆相交时的交点坐标问题，属于基础题目，联立方程求解即可．

练习册系列答案
相关题目
17．直线x+y+1=0与坐标轴围成的三角形的面积为（　　）
A．1B．2C．3D．$\frac{1}{2}$
18．设数列{an}为等差数列，若a1=1，求公差d取何值时，使得a1•a3+a2•a3最小．
15．在△ABC中，a=2，A=$\frac{π}{4}$，若此三角形有两解，则b的取值范围是（2，2$\sqrt{2}$）．
2．解方程：${C}_{18}^{x}$=${C}_{18}^{3x-6}$．
12．已知A={a+2，（a+1）2，a2+3a+3}，且1∈A，求实数2013a的值．
19．已知向量$\overrightarrow{m}$，$\overrightarrow{n}$的模分别为$\sqrt{2}$，2，且$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为45°，在△ABC中，$\overrightarrow{AB}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$，$\overrightarrow{AC}$=2$\overrightarrow{m}$-6$\overrightarrow{n}$，$\overrightarrow{BC}$=2$\overrightarrow{BD}$，则|$\overrightarrow{AD}$|=2$\sqrt{2}$．
16．根据下列条件分别写出直线的方程化为一般式方程：
（1）斜率为0，在y轴上的截距为2；
（2）经过A（-2，1），B（1，0）两点．
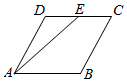
17．如图，在菱形ABCD中，AB=2，∠DAB=60°，E为CD的中点，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的值是（　　）
A．$\sqrt{7}$B．5C．$\sqrt{21}$D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网