题目内容
8.若直线l被圆C:x2+y2=2所截的弦长不小于2,下列方程表示的曲线中与直线l一定有公共点的是( )| A. | y=x2 | B. | (x-1)2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{2}+{y^2}=1$ |
分析 由题意知可以得到原点到直线的距离小于等于1,即直线上有一点到原点的距离小于等于1,在四个选项中只有这个点一定在椭圆内或椭圆上,得到结果.
解答 解:∵直线l被圆C:x2+y2=2所截的弦长不小于2,
∴原点到直线的距离小于等于1,
∴直线上有一点到原点的距离小于等于1,
在四个选项中只有这个点一定在椭圆内或椭圆上,
∴l与椭圆一定有公共点
故选D.
点评 本题考查直线与圆锥曲线之间的关系问题,本题解题的关键是当有一个点在一个封闭图形内部,则过这个点的直线一定与封闭曲线有交点.

练习册系列答案
相关题目
16.阅读如图的程序框图,运行相应的程序,若$f(x)=cos\frac{π}{3}x$,则输出的S的值为( )
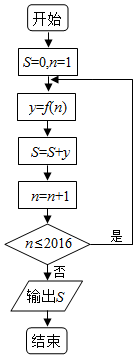

| A. | 0 | B. | 671.5 | C. | 671 | D. | 672 |
3.类比结论“平面内,垂直于同一条直线的两条直线互相平行”,在空间可得如下结论:
①垂直于同一条直线的两条直线平行;
②垂直于同一平面的两条直线互相平行;
③垂直于同一条直线的两个平面互相平行;
④垂直于同一平面的两个平面互相平行.
则正确结论的序号是( )
①垂直于同一条直线的两条直线平行;
②垂直于同一平面的两条直线互相平行;
③垂直于同一条直线的两个平面互相平行;
④垂直于同一平面的两个平面互相平行.
则正确结论的序号是( )
| A. | ②③ | B. | ②④ | C. | ②③④ | D. | ①②③④ |
13.已知函数f(x)=cos2x-sin2x,下列说法错误的是( )
| A. | f(x)的最小正周期为π | B. | x=$\frac{π}{2}$是f(x)的一条对称轴 | ||
| C. | f(x)在(-$\frac{π}{4}$,$\frac{π}{4}$)上单调递增 | D. | |f(x)|的值域是[0,1] |
17.分段函数f(x)=$\left\{\begin{array}{l}{a\sqrt{x}+b,x≥1}\\{xcos\frac{π}{2}x,x<1}\end{array}\right.$在x=1处可导,则( )
| A. | a=0,b=-1 | B. | a=2,b=1 | C. | a=-π,b=π | D. | a=0,b=0 |