题目内容
9.已知函数f(x)=x2-ax(a<0)的最小值为-$\frac{1}{4}$,执行如图所示的程序框图,则输出的k值是( )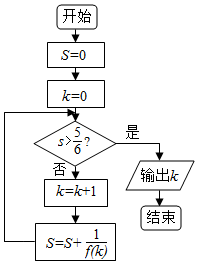
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
分析 根据二次函数的性质,结合函数f(x)=x2-ax(a<0)的最小值为-$\frac{1}{4}$,即可求出a的值,从而可求f(x)解析式,模拟运行程序,可得程序框图的功能是求S=1-$\frac{1}{k+1}$,继而求出k的值.
解答 解:f(x)=x2-ax=(x-$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$(a<0)的最小值为-$\frac{1}{4}$,
∴-$\frac{{a}^{2}}{4}$=-$\frac{1}{4}$,
∴a=-1,
∴f(x)=x2+x,
∴$\frac{1}{f(x)}$=$\frac{1}{x(x+1)}$=$\frac{1}{x}$-$\frac{1}{x+1}$,
∴从而模拟程序运行,可得程序框图的功能是求S=$\frac{1}{2}$+$\frac{1}{6}$+…+$\frac{1}{{k}^{2}+k}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{k}$-$\frac{1}{k+1}$=1-$\frac{1}{k+1}$>$\frac{5}{6}$时k的值,
解得k>5,
则输出的k值是6,
故选:C.
点评 本题考查二次函数的性质和最值得问题,还考查了程序框图和算法,考查了循环结构,属于基本知识的考查

练习册系列答案
相关题目
17.分段函数f(x)=$\left\{\begin{array}{l}{a\sqrt{x}+b,x≥1}\\{xcos\frac{π}{2}x,x<1}\end{array}\right.$在x=1处可导,则( )
| A. | a=0,b=-1 | B. | a=2,b=1 | C. | a=-π,b=π | D. | a=0,b=0 |
14.若集合M={x|log2(x-1)<-1},N={x|$\frac{1}{4}$≤($\frac{1}{2}$)x+1<1},则∁R(M∪N)=( )
| A. | {x|-1<x<2} | B. | {x|x≤-1或x$≥\frac{3}{2}$} | C. | {x|0<x<$\frac{3}{2}$} | D. | {x|x≤0或x≥2} |
1.设不等式组$\left\{\begin{array}{l}{x+2y-5≤0}\\{x≥-1}\\{y≥0}\end{array}\right.$,表示的平面区域为D,点A(3,0),原点O(0,0),在区域D内随机取一点M,则点M满足|MA|≥2|MO|的概率是( )
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{9}$ | D. | $\frac{π}{12}$ |