题目内容
已知f(x)是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设a=f(log47),b=f(log
3),c=f(21.6),则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、c<a<b |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:利用对数和指数幂的运算性质,结合函数单调性和奇偶性的性质是解决本题的关键.
解答:
解:∵f(x)是定义在(-∞,+∞)上的偶函数,
∴b=f(log
3)=b=f(-log23)=f(log23),
∵log23=log49>log47,21.6>2,
∴log47<log49<21.6,
∵在(-∞,0]上是增函数,
∴在[0,+∞)上为减函数,
则f(log47)>f(log49)>f(21.6),
即c<b<a,
故选:B
∴b=f(log
| 1 |
| 2 |
∵log23=log49>log47,21.6>2,
∴log47<log49<21.6,
∵在(-∞,0]上是增函数,
∴在[0,+∞)上为减函数,
则f(log47)>f(log49)>f(21.6),
即c<b<a,
故选:B
点评:本题主要考查函数值的大小比较,根据函数的奇偶性和单调性之间的关系以及对数的运算性质是解决本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
执行如图所示的程序框图,输出的S值为( )


| A、-6 | B、-10 | C、6 | D、10 |
已知a+2i=1+2bi(a,b∈R),其中i为虚数单位,则a+b=( )
| A、2 | B、-2 | C、1 | D、-1 |
等边△ABC的边长为2,D为AB的中点,E为线段AC上一动点,则
•
的取值范围是( )
| EB |
| ED |
| A、[2,9] | ||
B、[
| ||
C、[
| ||
D、[
|
为了得到函数y=
sinxcosx+sin2x-
的图象,可以将函数y=sin2x的图象( )
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
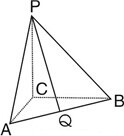 如图,三棱锥P-ABC中,PC,AC,BC两两互相垂直,AC=2,BC=4,PC=3,Q为AB中点,则线段PQ的长是( )
如图,三棱锥P-ABC中,PC,AC,BC两两互相垂直,AC=2,BC=4,PC=3,Q为AB中点,则线段PQ的长是( )A、
| ||
B、
| ||
C、
| ||
D、2
|
已知集合A={x|y=
,x∈R},B={y|y=x2+1,x∈R},则A∩B为( )
| 1-x2 |
| A、{1} | B、[0,+∞) |
| C、∅ | D、{(0,1)} |
 随机抽取某花场甲、乙两种树苗各10株,测量它们的高度(单位;cm),获得高度数据的茎叶图如图.给出以下关于甲、乙两种各10株树苗高度的结论:
随机抽取某花场甲、乙两种树苗各10株,测量它们的高度(单位;cm),获得高度数据的茎叶图如图.给出以下关于甲、乙两种各10株树苗高度的结论: