题目内容
甲、乙两人各进行3次射击,甲每次击中目标的概率为
,乙每次击中目标的概率为
.记甲击中目标的次数为X,乙击中目标的次数为Y.
(1)求X的分布列;
(2)求X和Y的数学期望.
| 1 |
| 2 |
| 2 |
| 3 |
(1)求X的分布列;
(2)求X和Y的数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)X的取值为0、1、2、3.X~B(3,
),由此能求出X分布列.
(2)由X~B(3,
),Y~B(3,
),能求出EX和EY.
| 1 |
| 2 |
(2)由X~B(3,
| 1 |
| 2 |
| 2 |
| 3 |
解答:
解:(1)X的取值为0、1、2、3.X~B(3,
),
P(X=k)=
(
)3,k=0,1,2,3.
X分布列为:
(2)因X~B(3,
),Y~B(3,
),
故EX=3×
=1.5,EY=3×
=2.
| 1 |
| 2 |
P(X=k)=
| C | k 3 |
| 1 |
| 2 |
X分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 2 |
| 3 |
故EX=3×
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查概率的求法,考查注意离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
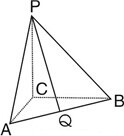 如图,三棱锥P-ABC中,PC,AC,BC两两互相垂直,AC=2,BC=4,PC=3,Q为AB中点,则线段PQ的长是( )
如图,三棱锥P-ABC中,PC,AC,BC两两互相垂直,AC=2,BC=4,PC=3,Q为AB中点,则线段PQ的长是( )A、
| ||
B、
| ||
C、
| ||
D、2
|
若x=-1是函数f(x)=ax3-3x的一个极值点,则a的值为( )
| A、-1 | B、-2 | C、1 | D、2 |
已知集合A={x|y=
,x∈R},B={y|y=x2+1,x∈R},则A∩B为( )
| 1-x2 |
| A、{1} | B、[0,+∞) |
| C、∅ | D、{(0,1)} |
在极坐标系中,点M(3,
)和点N(-3,
π)的位置关系是( )
| π |
| 3 |
| 2 |
| 3 |
| A、关于极轴所在直线对称 | ||
| B、重合 | ||
C、关于直线θ=
| ||
| D、关于极点对称 |
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD=90°,且AB=2AD=2DC=2PD=4,E为PA的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD=90°,且AB=2AD=2DC=2PD=4,E为PA的中点.