题目内容
曲线y=
在点M（
，0）处的切线斜率为（ ）
| sinx |
| sinx+cosx |
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，然后直接代入x=
求值．
| π |
| 4 |
解答：
解：∵y=
，
∴y′=
=
．
∴y′|x=
=
．
故选：A．
| sinx |
| sinx+cosx |
∴y′=
| cosx(sinx+cosx)-sinx(cosx-sinx) |
| (sinx+cosx)2 |
=
| 1 |
| (sinx+cosx)2 |
∴y′|x=
| π |
| 4 |
| 1 |
| 2 |
故选：A．
点评：本题考查了利用导数研究过曲线上某点处的切线方程，考查了基本初等函数的导数公式，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
执行如图所示的程序框图，输出的S值为（ ）
| A、-6 | B、-10 | C、6 | D、10 |
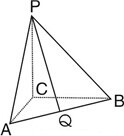如图，三棱锥P-ABC中，PC，AC，BC两两互相垂直，AC=2，BC=4，PC=3，Q为AB中点，则线段PQ的长是（ ）A、
| ||
B、
| ||
C、
| ||
D、2
|
随机抽取某花场甲、乙两种树苗各10株，测量它们的高度（单位；cm），获得高度数据的茎叶图如图．给出以下关于甲、乙两种各10株树苗高度的结论：不等式
+
-
≥0对x，y∈R+恒成立，则λ的取值范围是（ ）
| 1 |
| x |
| 1 |
| y |
| λ |
| x+y |
| A、（-∞，0] |
| B、（-∞，1） |
| C、（-∞，4] |
| D、（4，+∞） |
函数f（x）=2x-cosx的零点的个数为（ ）
| A、1个 | B、2个 |
| C、无穷多个 | D、0个 |
若x=-1是函数f（x）=ax3-3x的一个极值点，则a的值为（ ）
| A、-1 | B、-2 | C、1 | D、2 |
已知集合A={x|y=
，x∈R}，B={y|y=x2+1，x∈R}，则A∩B为（ ）
| 1-x2 |
| A、{1} | B、[0，+∞） |
| C、∅ | D、{（0，1）} |