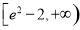题目内容
17.已知:直线a∥b,a∩平面α=P.求证:直线b与平面α相交.分析 假设直线b与平面a不相交(交点个数为0),从而推导出直线a∥平面a或直线a?平面a(交点无数个),与已知条件相悖,故假设不成立,由此能证明直线b与平面a相交.
解答 证明:用反证法.
假设直线b与平面a不相交(交点个数为0),
∴直线b∥平面a
又∵直线a∥直线b,
∴直线a∥平面a或直线a?平面a(交点无数个),
而由题意知a∩平面α=P,即直线a与平面a有且只有一个交点,
与已知条件相悖,故假设不成立,
∴直线b与平面a相交.
点评 本题考查线面相交的证明,是基础题,解题时要认真审题,注意空间思维能力的培养产反证法的合理运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
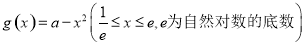 与
与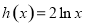 的图象上存在关于
的图象上存在关于 轴对称的点,则实数
轴对称的点,则实数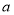 的取值范围是( )
的取值范围是( )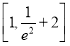 B.
B.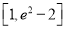 C.
C.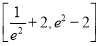 D.
D.