题目内容
5.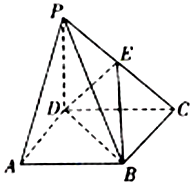 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PD⊥AB,PD⊥BC,且PD=1,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PD⊥AB,PD⊥BC,且PD=1,E为PC的中点.(1)求证:PA∥平面BDE;
(2)求直线PB与平面BDE所成角的正弦值.
分析 (1)连接AC,交BD于点O,连接OE,证明OE∥PA,然后证明PA∥平面BDE.
(2)以D为原点,分别以DA,DC,DP为x,y,z轴,建立空间直角坐标系,求出相关点的坐标,平面BDE的一个法向量,然后利用向量的数量积求解直线PB与平面BDE所成角的正弦值.
解答 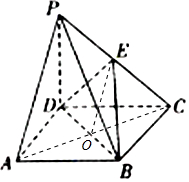 (1)证明:连接AC,交BD于点O,连接OE,则O是AC的中点,
(1)证明:连接AC,交BD于点O,连接OE,则O是AC的中点,
又因为E是PC的中点,所以OE是三角形PAC的中位线,所以OE∥PA,
∵OE?平面BDE,∴PA?平面BDE,
∴PA∥平面BDE.
(2)解:∵PD⊥AB,PD⊥BC,AB∩BC=B,∴PD⊥平面ABCD,
如图,以D为原点,分别以DA,DC,DP为x,y,z轴,
建立空间直角坐标系,
则D(0,0,0),B(1,1,0),P(0,0,1),$E(0,\frac{1}{2},\frac{1}{2})$,
∴$\overrightarrow{PB}=(1,1,-1)$,$\overrightarrow{DE}=(0,\frac{1}{2},\frac{1}{2})$,$\overrightarrow{DB}=(1,1,0)$,
设平面BDE的一个法向量为$\overrightarrow n=(x,y,z)$
由$\overrightarrow n⊥\overrightarrow{DE}$,$\overrightarrow n⊥\overrightarrow{DB}$得,$\left\{\begin{array}{l}\frac{1}{2}y+\frac{1}{2}z=0\\ x+y=0\end{array}\right.$,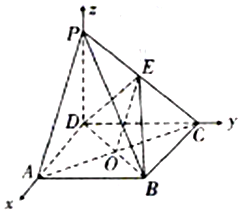
令x=1,则y=-1,z=1,
∴$\overrightarrow n=(1,-1,1)$,又∵$\overrightarrow{PB}=(1,1,-1)$,
∴$cos<\overrightarrow n,\overrightarrow{PB}>=\frac{{\overrightarrow n•\overrightarrow{PB}}}{{|\overrightarrow n|•|\overrightarrow{PB}|}}=\frac{-1}{{\sqrt{3}×\sqrt{3}}}=-\frac{1}{3}$,
∴直线PB与平面BDE所成角的正弦值为$\frac{1}{3}$.
点评 本题考查直线与平面平行,直线与平面所成角的求法,考查空间想象能力以及计算能力.

 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案| A. | f(x)是偶函数,单调递增区间是(0,+∞) | B. | f(x)是偶函数,单调递减区间是(-∞,1) | ||
| C. | f(x)是奇函数,单调递增区间是(-∞,0) | D. | f(x)是奇函数,单调递减区间是(-1,1) |
| A. | (0,1) | B. | (1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(0,1) |
| A. | -5 | B. | -4 | C. | $\frac{2}{3}$ | D. | 4 |
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{7\sqrt{3}}}{8}$ |