题目内容
15．函数f（x）=x-lnx的单调递减区间是（ ）| A． | （0，1） | B． | （0，+∞） | C． | （1，+∞） | D． | （-∞，0）∪（1，+∞） |
分析 求出函数的导数为y′，再解y'＜0得x的范围．结合函数的定义域，即可得到单调递减区间．
解答 解：函数y=x-lnx的导数为y=1-$\frac{1}{x}$，
令y′=1-$\frac{1}{x}$＜0，得x＜1
∴结合函数的定义域，得当x∈（0，1）时，函数为单调减函数．
因此，函数y=x-lnx的单调递减区间是（0，1）
故选：A．
点评 本题给出含有对数的基本函数，求函数的减区间，着重考查了利用导数研究函数的单调性和函数的定义域等知识，属于基础题．
练习册系列答案
孟建平名校考卷系列答案
相关题目
5．已知向量$\overrightarrow{a}$=（k，3），$\overrightarrow{b}$=（1，4），$\overrightarrow{c}$=（2，1）且（3$\overrightarrow{a}$-2$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则实数k=（ ）
| A． | -$\frac{9}{2}$ | B． | 0 | C． | 3 | D． | $\frac{1}{2}$ |
6．定义在R上的可导函数f（x），其导数为f′（x），则“f′（x）为偶函数”是“f（x）为奇函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示．假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km，试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式．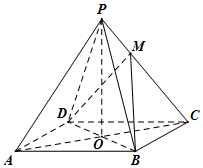
如图，已知四棱锥P-ABCD的底面是菱形，对角线AC，BD交于点O，OA=4，OB=3，OP=4，OP⊥底面ABCD，设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$（λ＞0）．
20．函数f（x）=x2-2lnx的单调减区间是（ ）
| A． | （0，1） | B． | （1，+∞） | C． | （-∞，-1）∪（0，1） | D． | （-1，0）∪（0，1） |
5．设a=ln2，b=log23，c=log3$\frac{1}{2}$，则a，b，c的大小关系是（ ）
| A． | a＞c＞b | B． | b＞c＞a | C． | b＞a＞c | D． | c＞b＞a |