题目内容
已知函数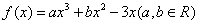 在点
在点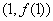 处的切线方程为
处的切线方程为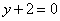 。
。
(1)求函数 的解析式;
的解析式;
(2)若对于区间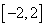 上用意两个自变量的值
上用意两个自变量的值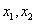 ,都有
,都有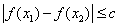 ,求实数
,求实数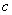 的最小值;
的最小值;
(3)若过点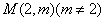 可作曲线
可作曲线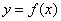 的三条切线,求实数
的三条切线,求实数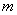 的取值范围。
的取值范围。
解:(1) ,依题意有
,依题意有 解得
解得 ,所以
,所以 。………………………………5分
。………………………………5分
(2)设 得
得 ,从而函数在
,从而函数在 和
和 上递增,在
上递增,在 上递减,故当
上递减,故当 时,
时, ,则对于区间
,则对于区间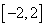 上用意两个自变量的值
上用意两个自变量的值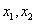 ,都有
,都有 ,所以
,所以 。所以
。所以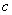 的最小值为4。………………………………10分
的最小值为4。………………………………10分
(3)因为点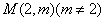 不在曲线上,所以设切点为
不在曲线上,所以设切点为 ,则
,则 。因为
。因为 ,所以切线的斜率为
,所以切线的斜率为 ,所以
,所以 ,化简得
,化简得 。因为过点
。因为过点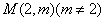 可作曲线
可作曲线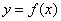 的三条切线,所以方程
的三条切线,所以方程 有三个不同的实数解,故函数
有三个不同的实数解,故函数 有三个不同的零点,则
有三个不同的零点,则 ,设
,设 ,得
,得 或
或 ,知函数
,知函数 在
在 和
和 上递增,在
上递增,在 上递减,则
上递减,则 ,解得
,解得

练习册系列答案
相关题目

 。
。 的单调区间;
的单调区间; ,当
,当 时,若对任意的
时,若对任意的 都有
都有 ,求实数
,求实数 的取值范围;
的取值范围; ﹤
﹤ 。
。 中,
中, ,
, ,过点D的直线分别交直线AB,AC于点M,N.若
,过点D的直线分别交直线AB,AC于点M,N.若 , 则
, 则 的最小值是 .
的最小值是 .
 在点
在点 处的切线方程为
处的切线方程为  ,
, , (
, ( ),在复平面内对应的点分别为
),在复平面内对应的点分别为 .
. 是纯虚数,求
是纯虚数,求 在复平面内对应的点位于第四象限,求
在复平面内对应的点位于第四象限,求 ,则
,则 的值为_________
的值为_________ ,推广到空间,棱长为a的正四面体内任一点到各个面距离之和为
,推广到空间,棱长为a的正四面体内任一点到各个面距离之和为  (a为常数)的定义域为
(a为常数)的定义域为 ,
,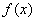 的最大值为6,则a等于( )
的最大值为6,则a等于( )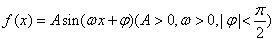 的部分图象如图所示.
的部分图象如图所示.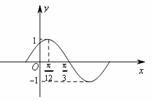 (1)求函数
(1)求函数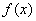 的表达式;
的表达式;