题目内容
己知函数
 。
。
⑴讨论函数 的单调区间;
的单调区间;
⑵设 ,当
,当 时,若对任意的
时,若对任意的 都有
都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)求证: ﹤
﹤ 。
。
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
解:(1)

当 时,递减区间为
时,递减区间为 ,递增区间为
,递增区间为 ;
;
当 时,递增区间为
时,递增区间为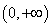 ;
;
当 时,递减区间为
时,递减区间为 ,递增区间为
,递增区间为 。------------4分
。------------4分
(2)当 时,
时,
由(1)知 时
时
对任意的 都有
都有 恒成立
恒成立
即 ,
, 恒成立
恒成立
即 ,
, 恒成立
恒成立
即 ,
, 恒成立
恒成立
令 ,则
,则 ,
,
即 在
在 上递增,故
上递增,故
所以 。---------------8分
。---------------8分
(3)当 时,
时,
由(1)知, 单调递增,则
单调递增,则 时,
时,
即
取 ,
,
则
故

。。。。。。 。。。。。。

上式叠加得:
即 。--------------12分
。--------------12分

练习册系列答案
相关题目
 (
( 为奇函数,且函数
为奇函数,且函数 的图象的两相邻对称轴之间的距离为
的图象的两相邻对称轴之间的距离为 .
. 的值;(2)将函数
的值;(2)将函数 个单位后,得到函数
个单位后,得到函数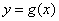 的图象,求函数
的图象,求函数 的单调递增区间.
的单调递增区间.  过圆
过圆 的圆心,且与直线
的圆心,且与直线 垂直,则直线
垂直,则直线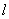 过抛物线
过抛物线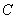 :
: 的焦点,且与
的焦点,且与 轴垂直,则直线
轴垂直,则直线 B.
B. C.
C. D.
D.
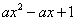 ﹥0在
﹥0在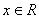 上恒成立,则
上恒成立,则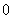 ﹤
﹤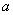 ﹤4;
﹤4;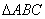 中,
中,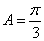 ,则
,则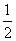 ﹤
﹤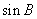 ﹤1;
﹤1;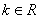 ,直线
,直线 与椭圆
与椭圆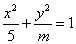 (
(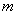 ﹥0)恒有公共点,则
﹥0)恒有公共点,则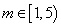 ;
;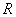 上的函数
上的函数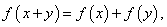 当
当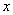 ﹤0时,
﹤0时,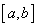 上有最小值
上有最小值 。
。  表示的点落在 ( )
表示的点落在 ( ) ,则
,则 =
= ,
, ,
, )
)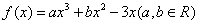 在点
在点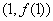 处的切线方程为
处的切线方程为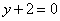 。
。 的解析式;
的解析式;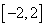 上用意两个自变量的值
上用意两个自变量的值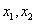 ,都有
,都有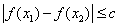 ,求实数
,求实数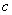 的最小值;
的最小值;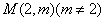 可作曲线
可作曲线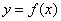 的三条切线,求实数
的三条切线,求实数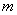 的取值范围。
的取值范围。