题目内容
设
，
是两个非零向量，则“
，
的夹角为钝角”是“
•
＜0”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：空间向量及应用,简易逻辑
分析：此命题可通过研究共线且反向的两个向量的内积来说明其必要性不成立．
解答：
解：充分性：“
，
的夹角为钝角”，则
•
=|
||
|cos＜
，
＞＜0，即“
•
＜0”，充分性成立；
必要性：当
，
共线且反向时，夹角为180°，不是钝角，但满足“
•
＜0”，必要性不成立；
故“
，
的夹角为钝角”是“
•
＜0”的充分不必要条件，
故选：A．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
必要性：当
| a |
| b |
| a |
| b |
故“
| a |
| b |
| a |
| b |
故选：A．
点评：本题考查命题的真假判断与应用，充要条件等基本知识，解题的关键是对每个问题涉及的基础知识有全面的了解，本题知识性强，题后要认真体会
练习册系列答案
相关题目
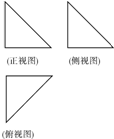已知某三棱锥的三视图均为腰长为 2的等腰直角三角形（如图），则该棱锥的表面积为（ ）A、6+2
| ||
B、6+4
| ||
C、12+4
| ||
D、8+4
|
已知双曲线
-
=1的焦点为（4，0），则此双曲线的渐近线方程是（ ）
| x2 |
| a2 |
| y2 |
| 4 |
A、
| ||
B、x±
| ||
C、
| ||
D、x±
|