题目内容
已知在平面直角坐标系中,曲线
(t为参数)与曲线
(θ为参数)相交于A、B两点.
(1)求点M(-1,2)到直线AB的距离.
(2)求线段AB的中点坐标.
|
|
(1)求点M(-1,2)到直线AB的距离.
(2)求线段AB的中点坐标.
考点:曲线与方程,参数方程化成普通方程
专题:圆锥曲线的定义、性质与方程
分析:求出参数方程对应的普通方程,
(1)画出图形,判断点M(-1,2)到直线AB的距离是用两点间距离公式还是利用点到直线的距离公式求解.
(2)联立直线与经过圆的圆心与AB直线垂直的直线方程,求解即可得到中点坐标.
(1)画出图形,判断点M(-1,2)到直线AB的距离是用两点间距离公式还是利用点到直线的距离公式求解.
(2)联立直线与经过圆的圆心与AB直线垂直的直线方程,求解即可得到中点坐标.
解答:
 解:曲线
解:曲线
(t为参数)的普通方程为:2x+y=1.直线分斜率为:-2.
曲线
(θ为参数)的普通方程为:(x+2)2+(y-1)2=9.圆的圆心(-2,1).
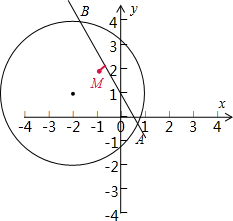
(1)直线与圆的方程对应的图形如图:
点M(-1,2)到直线AB的距离:d=
=
.
(2)经过圆的圆心与AB垂直的直线方程为:y-1=
(x+2)
,即x-2y+4=0,
所以
,解得x=-
,y=
,所求线段AB的中点坐标(-
,
).
 解:曲线
解:曲线
|
曲线
|
(1)直线与圆的方程对应的图形如图:
点M(-1,2)到直线AB的距离:d=
| |-2+2-1| | ||
|
| ||
| 5 |
(2)经过圆的圆心与AB垂直的直线方程为:y-1=
| 1 |
| 2 |
,即x-2y+4=0,
所以
|
| 2 |
| 5 |
| 9 |
| 5 |
| 2 |
| 5 |
| 9 |
| 5 |
点评:本题考查曲线与方程的应用,参数方程的应用,直线与圆的位置关系,点到直线的距离公式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将两枚质地均与透明且各面分别标有1,2,3,4的正四面体玩具各掷一次,设事件A={两个玩具底面点数不同},B={两个玩具底面点数至少出现一个2点},则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在区间(0,+∞)上不是增函数的函数是( )
| A、y=2-x | ||
| B、y=ln(x+1) | ||
C、y=-
| ||
| D、y=2x2+x+1 |
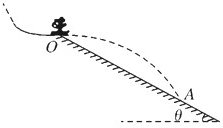 如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求:
如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求: