题目内容

（cos15°-cos75°）（sin75°+sin15°）=（　　）
A、
1
2
B、
2
2
C、
3
2
D、1
考点：二倍角的余弦,运用诱导公式化简求值
专题：三角函数的求值
分析：由诱导公式将sin75°、cos75°化为：cos15°和sin15°，代入原式利用二倍角的余弦公式化简、求值．
解答： 解：因为sin75°=sin（90°-15°）=cos15°，
cos75°=cos（90°-15°）=sin15°，
所以（cos15°-cos75°）（sin75°+sin15°）
=（cos15°-sin15°）（cos15°+sin15°）
=cos215°-sin215°=cos30°=
3
2
，
故选：C．
点评：本题考查诱导公式和二倍角的余弦公式的应用，注意角之间的关系，属于基础题．
练习册系列答案
相关题目
已知向量
OA
=（2，2），
OB
=（-4，1），点P在x轴的非负半轴上（O为原点）．
（1）当
PA
•
PB
取得最小值时，求
OP
的坐标；
（2）设∠APB=θ，当点P满足（1）时，求cosθ的值．
函数f（x）=xsinx2在区间[0，4]上的零点个数为（　　）
A、4B、5C、6D、7
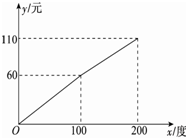某供电公司为了合理分配电力，采用分段计算电费政策，月用电量x（度）与相应电费y（元）之间的函数关系的图象如图所示．
（1）填空：月用电量为100度时，应交电费
 
元；
（2）当x≥100时，y与x之间的函数关系式为
 
；
（3）月用电量为260度时，应交电费
 
元．
已知函数f（x）=
|x-1|-2(|x|≤1)
1
1+x2
(|x|＞1)

（1）求函数f（x）的定义域；
（2）求f[f（
1
2
）]的值；
（3）若f（x）=
1
3
，求相应的x的值．
△ABC中角A，B，C所对边分别为a，b，c且1-cos2A-cos2B+cos2C=2
3
sinAsinB
（Ⅰ）求角C的大小；
（Ⅱ）若A∈（0，
2π
3
]，求y=2cos2
A
2
-sinB-1的值域．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），离心率为
1
2
，A1，A2是椭圆长轴的端点，长轴长为4，椭圆外一点M在直线x=-4上动，直线MA1与椭圆的另一交点为P，直线MA2与椭圆的另一交点为Q．
（1）求证：直线PQ过定点R，并求出R点坐标；
（2）R点关于y轴的对称点为S，直线QS与椭圆的另一交点为T，设
QR
=λ
RP
，
QS
=μ
ST
，求证：λ+μ为定值，并求出这个定值．
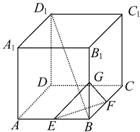在棱长为1的正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹的长度为（　　）
A、
1
2
B、
2
2
C、
3
3
D、
2
3
已知直三棱柱ABC-A1B1C1的六个顶点在球O上，若AB=3，AC=4，AB⊥AC，AA1=12，则球O的面积为（　　）
A、153πB、169π
C、10πD、90π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网