题目内容
二项式（3
+
）n的展开式中的各项系数和为P，所有二项式系数和为Q，若P+Q=272，求展开式中的常数项．
| 3 | x |
| 1 |
| x |
考点：二项式定理的应用
专题：二项式定理
分析：由条件求得P、Q，再根据P+Q=272，求得n=4，可得展开式的通项公式，再令通项公式中x的幂指数等于零，求得r的值，可得展开式中的常数项．
解答：
解：在二项式（3
+
）n的展开式中，令x=1，可得各项系数和为 P=4n，
所有二项式系数和为Q=2n，故由P+Q=272，可得（2n）2+2n-272=0，即n=4．
∵通项Tr+1=
34-rx
，∴4-4r=0，即r=1，∴常数项为108．
| 3 | x |
| 1 |
| x |
所有二项式系数和为Q=2n，故由P+Q=272，可得（2n）2+2n-272=0，即n=4．
∵通项Tr+1=
| C | r 4 |
| 4-4r |
| 3 |
点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，二项式系数的性质，注意各项系数和与各项的二项式系数和的区别，属于基础题．
练习册系列答案
相关题目
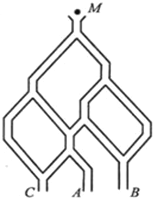如图，一个小球从 M处投入，通过管道自上而下落A或B或C．已知小球从每个叉口落入左右两个管道的可能性是相等的．某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为l，2，3等奖．
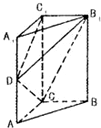如图，直三棱柱ABC-A1B1C1中，AA1=2AC=2BC，D是AA1的中点，CD⊥B1D．