题目内容
已知函数f(x)=x2lnx.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=kx-1有实数解,求实数k的取值范围.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=kx-1有实数解,求实数k的取值范围.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)首先考虑函数的定义域优先原则求出定义域,然后对函数求导,即可得到单调增区间,
(2)分离参数,构造函数g(x)=xlnx+
,求出函数的最小值即可.
(2)分离参数,构造函数g(x)=xlnx+
| 1 |
| x |
解答:
解:(1)由题意可知函数的定义域为:(0,+∞)
f′(x)=x(2lnx+1),
令f′(x)>0,得2lnx+1>0,即x>
令f′(x)<0,得2lnx+1<0,即0<x<
,
所以函数f(x)解:的递减区间是(0,
).函数的单调增区间为(
,+∞).
(2)由题意可得,关于x的方程f(x)=kx-1有实数解,
∴f(x)-kx+1=0,
即x2lnx-kx+1=0.
∴k=xlnx+
设g(x)=xlnx+
,
则g′(x)=lnx+
,
∴g′(1)=0,
当0<x<1时,g′(x)<0,g(x)单调递减,
当x>1时,g′(x)>0,g(x)单调递增,
所以当x=1时,g(x)min=g(1)=1,
所以k≥1,
故k的取值范围是[1,+∞)
f′(x)=x(2lnx+1),
令f′(x)>0,得2lnx+1>0,即x>
| ||
| e |
令f′(x)<0,得2lnx+1<0,即0<x<
| ||
| e |
所以函数f(x)解:的递减区间是(0,
| ||
| e |
| ||
| e |
(2)由题意可得,关于x的方程f(x)=kx-1有实数解,
∴f(x)-kx+1=0,
即x2lnx-kx+1=0.
∴k=xlnx+
| 1 |
| x |
设g(x)=xlnx+
| 1 |
| x |
则g′(x)=lnx+
| x2-1 |
| x2 |
∴g′(1)=0,
当0<x<1时,g′(x)<0,g(x)单调递减,
当x>1时,g′(x)>0,g(x)单调递增,
所以当x=1时,g(x)min=g(1)=1,
所以k≥1,
故k的取值范围是[1,+∞)
点评:本题主要考查了方程的根与函数零点间的关系,构造函数解决零点存在性问题的方法,导数在函数单调性和极值中的应用,转化化归的思想方法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
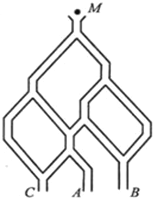 如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.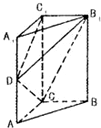 如图,直三棱柱ABC-A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.