题目内容
函数y＝logax＋1(a>0且a≠1)的图象恒过定点A，若点A在直线
＋
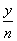－4＝0(m>0，n>0)上，则m＋n的最小值为( )
A．2＋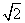
B．2 C．1 D．4
C
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
愉快的寒假南京出版社系列答案题目内容
函数y＝logax＋1(a>0且a≠1)的图象恒过定点A，若点A在直线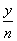＋－4＝0(m>0，n>0)上，则m＋n的最小值为( )
A．2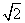＋ B．2 C．1 D．4
C
愉快的寒假南京出版社系列答案
，则不等式f(x2)<
＋
＋
，Q＝
，则( )
的图象交于P、Q两点，则线段PQ长的最小值是________．
若目标函数z＝ax＋by(a>0，b>0)的最大值为12，则
＋
的最小值为( )
B.
D．4