题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{|x+1|},x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$若实数x1、x2、x3、x4,满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4,则x1+x2+x3+x4的取值范围是( )| A. | (0,+∞) | B. | ($\frac{1}{2}$,$\frac{9}{4}$] | C. | (1,$\frac{9}{2}$] | D. | ($\frac{1}{2}$,$\frac{5}{4}$] |
分析 作出函数f(x)对应的图象,结合对数函数的性质以及函数的对称性,利用数形结合进行求解即可.
解答 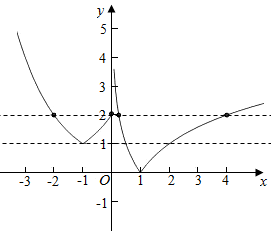 解:作出函数f(x)的图象如图
解:作出函数f(x)的图象如图
当x≤0时,二次函数的对称轴为x=-1,
若f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4,
当x=-1时,f(-1)=1,当x=0时,f(0)=2,
由|log2x|=2,得x=4或x=$\frac{1}{4}$,
由|log2x|=1,得x=2或x=$\frac{1}{2}$,
即$\frac{1}{4}$≤x3<$\frac{1}{2}$,2<x4<4,x1,x2关于x=-1对称,则x1+x2=-2,
则由f(x3)=f(x4)得|log2x3|=|log2x4|,
即-log2x3=log2x4,
则log2x2+log2x4=0,
即log2x3x4=0,
则x3x4=1,即x4=$\frac{1}{{x}_{3}}$,
则x1+x2+x3+x4=-2+x3+$\frac{1}{{x}_{3}}$,
∵y=-1+x3+$\frac{1}{{x}_{3}}$在$\frac{1}{4}$≤x3<$\frac{1}{2}$上是减函数,
∴当x3=$\frac{1}{2}$,y=-2+$\frac{1}{2}$+2=$\frac{1}{2}$,
当x3=$\frac{1}{4}$,y=-2+$\frac{1}{4}$+4=$\frac{9}{4}$,
即$\frac{1}{2}$<x1+x2+x3+x4≤$\frac{9}{4}$,
即x1+x2+x3+x4的取值范围是($\frac{1}{2}$,$\frac{9}{4}$],
故选:B.
点评 本题主要考查函数与方程的应用,利用数形结合以及对勾函数和一元二次函数的性质是解决本题的关键.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案| A. | $\frac{3}{5}$ | B. | 1 | C. | $\frac{\sqrt{5}}{3}$ | D. | 2 |
 如图,在直三棱柱ABC-A1B1C1中,已知AB=AC,M,N,P分别为BC,CC1,BB1的中点.求证:
如图,在直三棱柱ABC-A1B1C1中,已知AB=AC,M,N,P分别为BC,CC1,BB1的中点.求证: 如图,平面PAC⊥平面ABCD,DA=AB=BC=$\frac{1}{2}$CD=1.AB∥DC,∠CPD=90°.
如图,平面PAC⊥平面ABCD,DA=AB=BC=$\frac{1}{2}$CD=1.AB∥DC,∠CPD=90°.