题目内容
15. 如图,平面PAC⊥平面ABCD,DA=AB=BC=$\frac{1}{2}$CD=1.AB∥DC,∠CPD=90°.
如图,平面PAC⊥平面ABCD,DA=AB=BC=$\frac{1}{2}$CD=1.AB∥DC,∠CPD=90°.(1)证明:平面PAD⊥平面PCD;
(2)若二面角A-PC-D的大小为45°.求CP.
分析 (1)根据面面垂直的判定定理即可证明平面PAD⊥平面PCD;
(2)根据二面角平面角的定义,得到∠DPA=45°,根据直径三角形的边角关系即可求CP.
解答 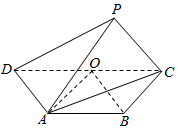 证明:(1)取CD的中点O,连接AO,OB,
证明:(1)取CD的中点O,连接AO,OB,
∵DA=AB=BC=$\frac{1}{2}$CD=1.
∴ABCO是菱形,
则OB⊥AC,
∵平面PAC⊥平面ABCD,
∴OB⊥平面PAC,则PC⊥OB,
∵OB∥AD,∴PC⊥AD,
∵∠CPD=90°,∴PC⊥PD,
∵PD∩AD=D,∴PC⊥平面PAD,
∵PC?平面PCD,∴平面PAD⊥平面PCD;
(2)∵PC⊥平面PAD,∴PC⊥PA,PC⊥PD,
则∠DPA是二面角A-PC-D的平面角,
∵二面角A-PC-D的大小为45°.
∴∠DPA=45,
∵AB=AC=1,∴AC=$\sqrt{3}$,
∵AD⊥平面PAD,∴AD⊥PA,
则PA=AD=1,在直角三角形APC中,
PC=$\sqrt{A{C}^{2}-A{P}^{2}}$=$\sqrt{3-1}$=$\sqrt{2}$.
点评 本题主要考查面面垂直的判断,以及二面角的应用,根据相应的定定理以及二面角的定义找出二面角的平面角是解决本题的关键.

练习册系列答案
相关题目
5.若复数z满足(1+2i)z=(1-i),则|z|=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\sqrt{10}$ |
10.从1,2,3,…,7共7个数字中任取3个不同的数字,则这3个数字由小到大可组成等差数列的概率为( )
| A. | $\frac{11}{35}$ | B. | $\frac{9}{35}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{7}$ |
20.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{|x+1|},x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$若实数x1、x2、x3、x4,满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4,则x1+x2+x3+x4的取值范围是( )
| A. | (0,+∞) | B. | ($\frac{1}{2}$,$\frac{9}{4}$] | C. | (1,$\frac{9}{2}$] | D. | ($\frac{1}{2}$,$\frac{5}{4}$] |
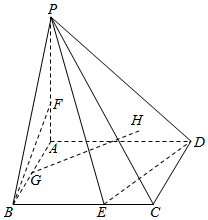 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,E、F、G分别为线段BC、PA、AB上的点,H为△PCD的重心,PA=AB=3,FA=BG=CE=1.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,E、F、G分别为线段BC、PA、AB上的点,H为△PCD的重心,PA=AB=3,FA=BG=CE=1.