题目内容
已知直线a、b、c和平面α、β,则下列命题中真命题的是 .
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a⊥c;
③若a、b异面,b、c异面,则a、c异面;
④若a∥α,b∥α,则a∥b;
⑤若a∥α,a∥β,且α∩β=b,则a∥b.
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a⊥c;
③若a、b异面,b、c异面,则a、c异面;
④若a∥α,b∥α,则a∥b;
⑤若a∥α,a∥β,且α∩β=b,则a∥b.
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①,利用公理4(平行线的传递性)可判断①;
②,利用空间中直线与直线的平行与垂直的位置关系,可判断②;
③,作正方体图形,数形结合可判断③;
④,利用空间线面平行的位置关系,可判断④;
⑤利用线面平行的性质定理与公理4可判断⑤.
②,利用空间中直线与直线的平行与垂直的位置关系,可判断②;
③,作正方体图形,数形结合可判断③;
④,利用空间线面平行的位置关系,可判断④;
⑤利用线面平行的性质定理与公理4可判断⑤.
解答:
解:①,若a∥b,b∥c,则a∥c,由公理4(平行线的传递性)知①正确;
②,若a⊥b,b⊥c,则a不一定与c垂直,可能a∥c,故②错误;
③,如图,在正方体中,

a、b异面,b、c异面,a、c共面,故③错误;
④若a∥α,b∥α,则可能a与b相交,也可能a与b异面,也可能a∥b,故④错误;
⑤若a∥α,a∥β,且α∩β=b,由线面平行的性质定理及平行线的传递性可知a∥b,故⑤正确;
故答案为:①⑤.
②,若a⊥b,b⊥c,则a不一定与c垂直,可能a∥c,故②错误;
③,如图,在正方体中,

a、b异面,b、c异面,a、c共面,故③错误;
④若a∥α,b∥α,则可能a与b相交,也可能a与b异面,也可能a∥b,故④错误;
⑤若a∥α,a∥β,且α∩β=b,由线面平行的性质定理及平行线的传递性可知a∥b,故⑤正确;
故答案为:①⑤.
点评:本题考查空间直线与直线的位置关系、直线与平面平行的性质定理的应用,考查空间想象能力与作图能力,属于中档题.

练习册系列答案
相关题目
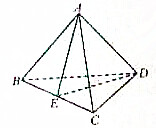 在所有棱长均为2的四面体ABCD中,E是BC的中点,写出四面体中与平面AED垂直的面,并说明理由.
在所有棱长均为2的四面体ABCD中,E是BC的中点,写出四面体中与平面AED垂直的面,并说明理由.