题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2作x轴的垂线交椭圆C于点P,若sin∠PF1F2=$\frac{1}{3}$,则( )| A. | a=$\sqrt{2}$b | B. | a=2b | C. | a=$\sqrt{3}$b | D. | a=3b |
分析 把x=c代入可得,解得y,利用sin∠PF1F2=$\frac{1}{3}$,即可得出.
解答 解:把x=c代入椭圆方程,解得y=±$\frac{{b}^{2}}{a}$,
∵sin∠PF1F2=$\frac{1}{3}$,∴tan∠PF1F2=$\frac{1}{2\sqrt{2}}$,
∴$\frac{\frac{{b}^{2}}{a}}{2c}$=$\frac{1}{2\sqrt{2}}$,
∴a4-a2b2-2b4=0,∴a=$\sqrt{2}b$,
故选A.
点评 本题了考查了椭圆的标准方程及其性质、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
13.已知函数f(x)=xex-1-a,则下列说法正确的是( )
| A. | 当a<0时,f(x)有两个零点 | B. | 当a=0时,f(x)无零点 | ||
| C. | 当0<a<1时,f(x)有小于1的零点 | D. | 当a>1时,f(x)有大于a的零点 |
13.已知空间两不同直线m、n,两不同平面α、β,下列命题正确的是( )
| A. | 若m∥α且n∥α,则m∥n | B. | 若m⊥β且m⊥n,则n∥β | ||
| C. | 若m⊥α且m∥β,则α⊥β | D. | 若m不垂直于α,且n?α则m不垂直于n |
9.若复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,其中i为虚数单位,则a=( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
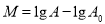 ,其中,
,其中,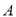 是被测地震的最大振幅,
是被测地震的最大振幅,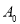 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。 ,
, 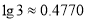 )
) 某空间几何体的三视图如图所示,其中正视图是长方形,侧视图是一个等腰梯形,则该几何体的体积是6,表面积是15+4$\sqrt{5}$.
某空间几何体的三视图如图所示,其中正视图是长方形,侧视图是一个等腰梯形,则该几何体的体积是6,表面积是15+4$\sqrt{5}$. 从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: