题目内容
17.在四面体ABCD中,A-BD-C为直二面角,AB=AD=5,BC=CD=DB=6,则直线AC与平面BCD所成角的正弦值为$\frac{4\sqrt{43}}{43}$.分析 取BD中点O,连结AO,CO,则AO⊥平面BDC,AO⊥BD,CO⊥BD,从而∠AOC是二面角A-BD-C 平面角,且∠AOC=90°,由AO⊥平面BDC,知∠ACO是直线AC与平面BCD所成角,由此能求出直线AC与平面BCD所成角的正弦值.
解答 解: 如图,取BD中点O,连结AO,CO,
如图,取BD中点O,连结AO,CO,
∵在四面体ABCD中,A-BD-C为直二面角,AB=AD=5,BC=CD=DB=6,
∴AO⊥平面BDC,AO⊥BD,CO⊥BD,
∴∠AOC是二面角A-BD-C 平面角,且∠AOC=90°,
∵AO⊥平面BDC,∴∠ACO是直线AC与平面BCD所成角,
∵AB=AD=5,BC=CD=DB=6,
∴AO=$\sqrt{{5}^{2}-{3}^{2}}$=4,CO=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,AC=$\sqrt{16+27}$=$\sqrt{43}$,
∴sin∠ACO=$\frac{AO}{AC}$=$\frac{4}{\sqrt{43}}=\frac{4\sqrt{43}}{43}$.
∴直线AC与平面BCD所成角的正弦值为$\frac{4\sqrt{43}}{43}$.
故答案为:$\frac{4\sqrt{43}}{43}$.
点评 本题考查线面角的正弦值的求法;考查逻辑推理与空间想象能力,运算求解能力;考查数形结合、化归转化思想.是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
5.已知全集U={1,2,3,4,5,6},集合P={1,3,5},Q={1,2,4},则(∁UP)∩Q=( )
| A. | {1} | B. | {2,4} | C. | {2,4,6} | D. | {1,2,4,6} |
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2作x轴的垂线交椭圆C于点P,若sin∠PF1F2=$\frac{1}{3}$,则( )
| A. | a=$\sqrt{2}$b | B. | a=2b | C. | a=$\sqrt{3}$b | D. | a=3b |
4.若直线y=kx+2k与曲线$y=\sqrt{1-{x^2}}$有两个不同的交点,则k的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $[{0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $[{0,\sqrt{3}})$ |
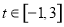 ,则输出的s属于( )
,则输出的s属于( )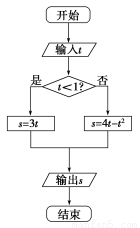
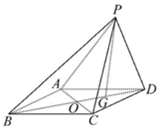 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.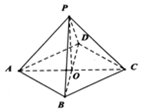 如图,在边长为2的菱形ABCD中,∠BAD=60°,O为AC的中点,点P为平面ABCD外一点,且平面PAC⊥平面ABCD,PO=1,PA=2.
如图,在边长为2的菱形ABCD中,∠BAD=60°,O为AC的中点,点P为平面ABCD外一点,且平面PAC⊥平面ABCD,PO=1,PA=2. 已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.
已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.