题目内容
18．已知椭圆的焦点是F1、F2，P是椭圆的一个动点，如果M是线段F1P的中点，则动点M的轨迹是（ ）| A． | 圆 | B． | 椭圆 | C． | 双曲线的一支 | D． | 抛物线 |
分析 设P（acosθ，bsinθ），由F1（-c，0），知线段PF1的中点M（$\frac{2cosθ-c}{2}$，$\frac{bsinθ}{2}$），由此求出线段PF1的中点M的轨迹是椭圆．
解答 解：由题意的参数方程可设P（acosθ，bsinθ），
∵F1（-c，0），∴线段PF1的中点M（$\frac{2cosθ-c}{2}$，$\frac{bsinθ}{2}$），
∴x=$\frac{2cosθ-c}{2}$，y=$\frac{bsinθ}{2}$，
∴cosθ=$\frac{2x+c}{a}$，sinθ=$\frac{2y}{b}$，
∴点P的轨迹方程为$\frac{（2x+c）^{2}}{{a}^{2}}$+$\frac{4{y}^{2}}{{b}^{2}}$=1，
∴线段PF1的中点M的轨迹是椭圆．
故选：B．
点评 本题考查点的轨迹方程的求法，是中档题，解题时要认真审题，注意椭圆的参数方程的合理运用．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
9．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在某一周期内的图象时，列表并填入了部分数据，如表：
（Ⅰ）根据如表求出函数f（x）的解析式；
（Ⅱ）设△ABC的三内角A，B，C的对边分别为a，b，c，且f（A）=$\sqrt{3}$，a=3，S为△ABC的面积，求S+3$\sqrt{3}$cosBcosC的最大值．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{π}{3}$ | x2 | $\frac{7π}{3}$ | x3 |
| y | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
（Ⅱ）设△ABC的三内角A，B，C的对边分别为a，b，c，且f（A）=$\sqrt{3}$，a=3，S为△ABC的面积，求S+3$\sqrt{3}$cosBcosC的最大值．
3．为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
（Ⅰ）求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}{y}_{i}）-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}{y}_{i}）-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
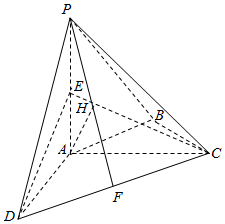如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA=45°，AP=AD=AC=2，E、F、H分别为PA、CD、PF的中点．