题目内容
17.实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≤0\\ x+3y-3≥0\end{array}\right.$,则z=|x+y+1|的最大值为( )| A. | 4 | B. | $2\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | 2 |
分析 作出不等式组对应的平面区域,z=|x+y+1|=$\sqrt{2}$•$\frac{|x+y+1|}{\sqrt{2}}$=$\sqrt{2}$d,转化为点到直线的距离进行求解即可.
解答 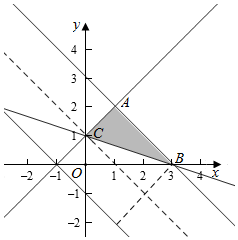 解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
z=|x+y+1|=$\sqrt{2}$•$\frac{|x+y+1|}{\sqrt{2}}$,
则$\frac{|x+y+1|}{\sqrt{2}}$的几何意义为区域内的点到直线x+y+1=0的距离d,
即d=$\frac{|x+y+1|}{\sqrt{2}}$,
由图象知AB到直线x+y+1=0的距离最大,
此时d=$\frac{|-3-1|}{\sqrt{2}}=\frac{4}{\sqrt{2}}$,
则z的最大值为$\sqrt{2}$•$\frac{4}{\sqrt{2}}$=4,
故选:A.
点评 本题主要考查线性规划的应用,根据不等式的关系转化为点到直线的距离是解决本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
7.△ABC中,tanA,tanB是方程6x2-5x+1=0的两根,则tanC=( )
| A. | -1 | B. | 1 | C. | $-\frac{5}{7}$ | D. | $\frac{5}{7}$ |
9.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入了部分数据,如表:
(Ⅰ)根据如表求出函数f(x)的解析式;
(Ⅱ)设△ABC的三内角A,B,C的对边分别为a,b,c,且f(A)=$\sqrt{3}$,a=3,S为△ABC的面积,求S+3$\sqrt{3}$cosBcosC的最大值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{π}{3}$ | x2 | $\frac{7π}{3}$ | x3 |
| y | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
(Ⅱ)设△ABC的三内角A,B,C的对边分别为a,b,c,且f(A)=$\sqrt{3}$,a=3,S为△ABC的面积,求S+3$\sqrt{3}$cosBcosC的最大值.
 已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,其短轴的下端点在抛物线x2=4y的准线上.
已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,其短轴的下端点在抛物线x2=4y的准线上.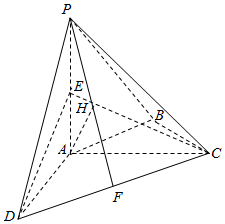 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.