题目内容
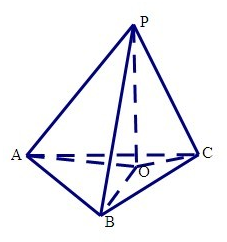
过三角形ABC所在平面外的一点P,作PO⊥平面α,垂足为O,连PA、PB、PC,则下列命题
①若PA=PB=PC,∠C=90°,则O是△ABC的边AB的中点;
②若PA=PB=PC,则O是三角形ABC的外心;
③若PA⊥PB,PB⊥PC,PC⊥PA,则O是三角形ABC的重心.
正确命题是( )
①若PA=PB=PC,∠C=90°,则O是△ABC的边AB的中点;
②若PA=PB=PC,则O是三角形ABC的外心;
③若PA⊥PB,PB⊥PC,PC⊥PA,则O是三角形ABC的重心.
正确命题是( )
| A、①②③ | B、①② | C、①③ | D、②③ |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:应用直线与平面垂直的判定和性质,平面几何中三角形的重心、垂心和外心的概念即可解决.
解答:
解:过三角形ABC所在平面外的一点P,作PO⊥平面α,垂足为O,连PA、PB、PC,
若PA=PB=PC,连接OA,OB,OC,则OA=OB=OC,则O为三角形ABC的外心;又若∠C=90°,则O为AB的中点.
故①②正确.
若PA⊥PB,PB⊥PC,PC⊥PA,则PA⊥平面PBC,从而PA⊥BC,
又PO⊥平面ABC,则PO⊥BC,所以BC⊥平面PAO,从而BC⊥AO,
同理AB⊥CO,AC⊥BO,故O为三角形的垂心,故③错,应改为垂心.
故选:B
若PA=PB=PC,连接OA,OB,OC,则OA=OB=OC,则O为三角形ABC的外心;又若∠C=90°,则O为AB的中点.
故①②正确.
若PA⊥PB,PB⊥PC,PC⊥PA,则PA⊥平面PBC,从而PA⊥BC,
又PO⊥平面ABC,则PO⊥BC,所以BC⊥平面PAO,从而BC⊥AO,
同理AB⊥CO,AC⊥BO,故O为三角形的垂心,故③错,应改为垂心.
故选:B

点评:本题主要考查空间的线面位置关系--垂直,解题时要结合平面几何的基础知识,同时考查逻辑推理能力,是一道基础题.

练习册系列答案
相关题目
下列命题中正确的是( )
A、当x>0且x≠1时,lgx+
| ||||||
B、当x>0,
| ||||||
C、当0<θ<
| ||||||
D、当0<x≤2时,x-
|
已知函数y=f(x)是偶函数,y=f(x-2)在[0,2]上单调递减,设a=f(0),b=f(2),c=f(-1),则( )
| A、a<c<b |
| B、a<b<c |
| C、b<c<a |
| D、c<b<a |
过两点A(4,y),B(2,-3)的直线的倾斜角是135°,则y=( )
| A、5 | B、-5 | C、1 | D、-1 |
下列命题中正确的是( )
A、“cosα=
| ||||
| B、函数y=f(x)在区间(a,b)内有零点,则f(a)•f(b)<0 | ||||
| C、数列{an}是等比数列的充要条件是an+12=anan+2(n∈N*) | ||||
| D、命题“?x∈R,2x>0”的否定是“?x∈R,2x≤0”. |
y=-3与y=sin3x的交点个数是( )
| A、0 | B、1 | C、2 | D、无数个 |