题目内容
3.设关于x,y的不等式组$\left\{\begin{array}{l}{2x-y+1≥0}\\{x-m≤0}\\{y+m≥0}{\;}\end{array}\right.$表示的平面区域内存在点P(x0,y0)满足$\frac{|3{x}_{0}-4{y}_{0}-12|}{5}$=1,则实数m的取值范围是( )| A. | [1,+∞) | B. | $[\frac{17}{7},+∞)$ | C. | $[1,\frac{17}{7}]$ | D. | $(-∞,\frac{17}{7}]$ |
分析 作出不等式组对应的平面区域,由|3x-4y-12|=5得d=$\frac{|3x-4y-12|}{5}$=1,即d的几何意义是区域内的点到直线3x-4y-12=0的距离等于1,利用数形结合进行求解即可.
解答 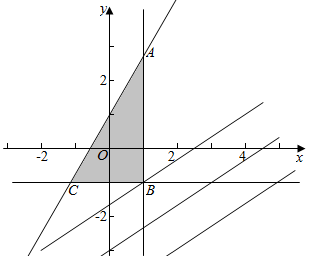 解:作出不等式组对应的平面如图:交点B坐标为(m,-m),(m>0)
解:作出不等式组对应的平面如图:交点B坐标为(m,-m),(m>0)
直线2x-y+1=0得y=2x+1,
由|3x-4y-12|=5得$\frac{|3x-4y-12|}{5}$=1,
设d=$\frac{|3x-4y-12|}{5}$,
则d的几何意义是区域内的点到直线3x-4y-12=0的距离等于1,
设到直线3x-4y-12=0的距离等于1的直线为3x-4y+c=0,
则$\frac{|c+12|}{5}$=1,得c=-7或c=-17.
要使平面区域内存在点P(x0,y0)满足|3x-4y-12|=5,
则点B(m,-m)必在直线3x-4y-7=0的下方,
即3m+4m-7≥0,解得m≥1.
故m的取值范围是:[1,+∞).
故选:A.
点评 本题主要考查线性规划的基本应用,利用数形结合是解决本题的关键,综合性较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.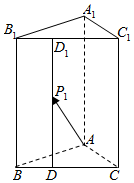 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )| A. | $\frac{\sqrt{10}}{6}$ | B. | $\frac{\sqrt{10}}{4}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{2}$ |
13.复数z=$\frac{2+i}{1-2i}$的虚部为( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{5}{3}$i | C. | 1 | D. | i |
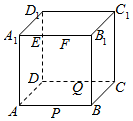 如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法:
如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法: