题目内容
14.若x,y满足约束条件$\left\{\begin{array}{l}{y≥1}\\{2x-y-1≥0}\\{x+y-a≤0}\end{array}\right.$,且z=3x-2y+3的最小值为2,则实数a的值为8.分析 由题意作出其平面区域,判断z=3x-2y+3的最小值为2时,结果可行域的点,求出点的坐标;代入x+y-a=0从而可得a.
解答 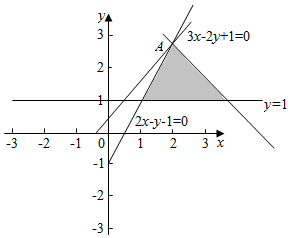 解:由题意作出x,y满足约束条件$\left\{\begin{array}{l}{y≥1}\\{2x-y-1≥0}\\{x+y-a≤0}\end{array}\right.$平面区域,
解:由题意作出x,y满足约束条件$\left\{\begin{array}{l}{y≥1}\\{2x-y-1≥0}\\{x+y-a≤0}\end{array}\right.$平面区域,
z=3x-2y+3的最小值为2,说明z=3x-2y+3经过图形中的A时直线的截距最大,z取得最小值.
结合图象可得,$\left\{\begin{array}{l}{3x-2y+1=0}\\{2x-y-1=0}\end{array}\right.$;
解得,x=3,y=5;
故直线x+y-a=0过点(3,5);
故a=8;
故答案为:8.
点评 本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
2.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点($\frac{a}{2}$,0)到直线l的距离d≥$\frac{1}{5}$c,则双曲线的离心率e的取值范围是( )
| A. | [$\frac{3}{2}$,2] | B. | [$\frac{\sqrt{5}}{2}$,2] | C. | [$\frac{3}{2}$,$\sqrt{5}$] | D. | [$\frac{\sqrt{5}}{2}$,$\sqrt{5}$] |
3.设关于x,y的不等式组$\left\{\begin{array}{l}{2x-y+1≥0}\\{x-m≤0}\\{y+m≥0}{\;}\end{array}\right.$表示的平面区域内存在点P(x0,y0)满足$\frac{|3{x}_{0}-4{y}_{0}-12|}{5}$=1,则实数m的取值范围是( )
| A. | [1,+∞) | B. | $[\frac{17}{7},+∞)$ | C. | $[1,\frac{17}{7}]$ | D. | $(-∞,\frac{17}{7}]$ |
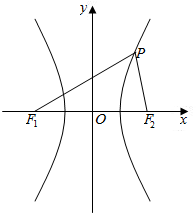 已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.
已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.