题目内容
12.求点A(0,2)与双曲线x2-y2=1上点的最小距离.分析 设双曲线上的点P(x,y),根据两点间的距离公式,利用消元法转化为关于y的一元二次函数进行求解即可.
解答 解:设双曲线上的点P(x,y),
则|AP|2=x2+(y-2)2=1+y2+(y-2)2=2y2-4y+5=2(y-1)2+3,
则当y=1时,|AP|2=2(y-1)2+3,取得最小值此时|AP|2=3,
则|AP|=$\sqrt{3}$,
即点A(0,2)与双曲线x2-y2=1上点的最小距离是$\sqrt{3}$.
点评 本题主要考查双曲线的性质,利用根据两点间的距离公式,利用消元法转化为关于y的一元二次函数是解决本题的关键.

练习册系列答案
相关题目
3.设关于x,y的不等式组$\left\{\begin{array}{l}{2x-y+1≥0}\\{x-m≤0}\\{y+m≥0}{\;}\end{array}\right.$表示的平面区域内存在点P(x0,y0)满足$\frac{|3{x}_{0}-4{y}_{0}-12|}{5}$=1,则实数m的取值范围是( )
| A. | [1,+∞) | B. | $[\frac{17}{7},+∞)$ | C. | $[1,\frac{17}{7}]$ | D. | $(-∞,\frac{17}{7}]$ |
20.已知函数f(x)=x3-3ax+$\frac{1}{4}$,若x轴为曲线y=f(x)的切线,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{3}{4}$ | D. | $\frac{1}{4}$ |
7.在腰长为2的等腰直角三角形内任取一点,则使得该点到此三角形的三个顶点的距离都不小于1的概率为( )
| A. | 1-$\frac{π}{2}$ | B. | 1-$\frac{π}{4}$ | C. | 1-$\frac{π}{8}$ | D. | 1-$\frac{π}{16}$ |
17.如图中的程序框图表示求三个实数a,b,c中最大数的算法,那么在空白的判断框中,应该填入( )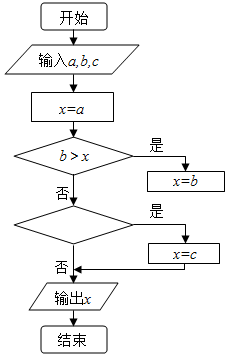

| A. | a>x | B. | b>x | C. | c<x | D. | c>x |
4.在等差数列{an}中,a5+a6=10,则其前10项和S10的值是( )
| A. | 10 | B. | 50 | C. | 60 | D. | 100 |
1.已知双曲线C的左右焦点为F1,F2,P双曲线右支上任意一点,若以F1为圆心,以$\frac{1}{2}$|F1F2|为半径的圆与以P为圆心,|PF2|为半径的圆相切,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | $\sqrt{3}$ |
2.如图是一个算法的程序框图,该算法所输出的结果是( )


| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |