题目内容
14.若小球自由落体的运动方程为s(t)=$\frac{1}{2}g{t^2}$(g为常数),该小球在t=1到t=3的平均速度为$\overline{v}$,在t=2的瞬时速度为v2,则$\overline{v}$和v2关系为( )| A. | $\overline{v}$>v2 | B. | $\overline{v}$<v2 | C. | $\overline{v}$=v2 | D. | 不能确定 |
分析 求函数的导数,根据导数的物理意义进行求解即可.
解答 解:平均速度为$\overline{v}$=$\frac{s(3)-s(1)}{3-1}$=$\frac{\frac{1}{2}g({3}^{2}-{1}^{2})}{2}$=2g,
∵s(t)=$\frac{1}{2}g{t^2}$,
∴s′(t)=gt,
t=2的瞬时速度为v2,
∴v2=s′(2)=g×2=2g,
∴$\overline{v}$=v2
故选:C.
点评 本题主要考查导数的计算和函数的变化率,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$的焦距等于( )
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
5.某程序框图如图所示,若该程序运行后输出的值是1,则正整数n的值是( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取( )名学生.
| A. | 40 | B. | 50 | C. | 60 | D. | 70 |
9.复数z=1-2i的虚部是( )
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |
6.设集合A={x∈Z|-1≤x<3},集合B={0,1,2,3},则A∪B中元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3.若cos($\frac{π}{6}$-α)=$\frac{3}{5}$,则cos($\frac{5π}{6}$+α)的值是( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
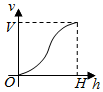
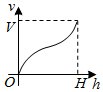
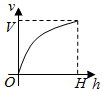
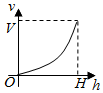
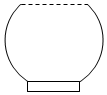 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )