题目内容
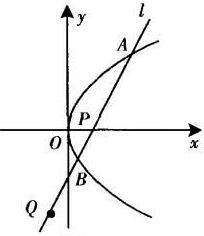如图，已知P为抛物线y2=4x的焦点，过点P的直线l与抛物线交于A，B两点，若点Q在直线AB上，且满足|| PA |
| QB |
| QA |
| PB |
考点：抛物线的简单性质
专题：证明题,直线与圆,圆锥曲线的定义、性质与方程
分析：求出抛物线的焦点和准线，过A作AK准线于K，作BL垂直准线于L．设直线AB与抛物线的准线交于Q'，运用抛物线的定义，以及平行线分线段成比例的性质，结合条件证明Q与Q'重合即可．
解答：
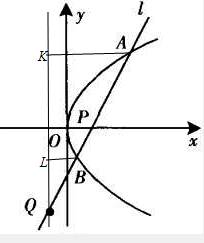证明：抛物线y2=4x的焦点P（1，0），准线为x=-1，
过A作AK准线于K，作BL垂直准线于L．
设直线AB与抛物线的准线交于Q'，
则由抛物线的定义，可得，
|
|=|
|，|
|=|
|，
在三角形AKQ'中，由平行线分线段成比例，可得，
=
，
由于|
|•|
|=|
|•|
|，
即为
=
，即有
=
，
即Q与Q'重合，则Q总在定直线x=-1上．
证明：抛物线y2=4x的焦点P（1，0），准线为x=-1，过A作AK准线于K，作BL垂直准线于L．
设直线AB与抛物线的准线交于Q'，
则由抛物线的定义，可得，
|
| PA |
| AK |
| PB |
| BL |
在三角形AKQ'中，由平行线分线段成比例，可得，
|
| ||
|
|
|
| ||
|
|
由于|
| PA |
| QB |
| QA |
| PB |
即为
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
即Q与Q'重合，则Q总在定直线x=-1上．
点评：本题考查抛物线的方程、定义和性质，考查平行线分线段成比例的性质，属于中档题．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
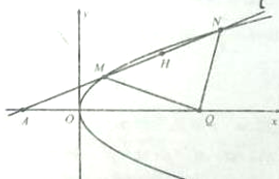已知抛物线y2=4x，直线l：y=kx+2（k＞0）与抛物线C交于M、N两点，与x轴交于点A，H 为MN的中点，O为坐标原点．