题目内容
在△ABC中，BC=6
，BC边上中线AD=3，则
•
= ．
| 3 |
| AB |
| AC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量的加法的几何意义和向量的运算计算即可得到答案
解答：
解：如图所示，
∵BC=6
，BC边上中线AD=3，
∴
•
=
•
=（
+
）（
+
）=
•
+
•
+
•
+
•
=-|
|2+|
|2=-（
）2+32=-18，
故答案为：-18
解：如图所示，∵BC=6
| 3 |
∴
| AB |
| AC |
| BA |
| CA |
| BD |
| DA |
| CD |
| DA |
| BD |
| CD |
| BD |
| DA |
| DA |
| CD |
| DA |
| DA |
| BD |
| DA |
6
| ||
| 2 |
故答案为：-18
点评：本题主要考查了向量的加法的几何意义，属于基础题
练习册系列答案
相关题目
已知函数f（x）是定义在R上的奇函数，若g（x）=f（x+1）+5，g（x）=f（x+1）+5，g′（x）为g（x）的导函数，对?x∈R，总有g′（x）＞2x，则g（x）＜x2+4的解集为（ ）
| A、（-∞，-1） |
| B、（-∞，1） |
| C、R |
| D、（-1，+∞） |
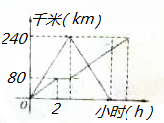甲，乙两车在连通A，B，C三地的公路上行驶，甲车从A地出发匀速向C地行驶，中途到达B地并在B地停留1小时后按原速驶向C地；同时乙车从C地出发匀速向A地行驶，到达A地后，立即按原路原速返回到C地并停留．在两车行驶的过程中，甲，乙两车距各自出发地的路程y（千米）与行驶时间x（小时）之间的函数关系如图所示，请结合图象回答下列问题：
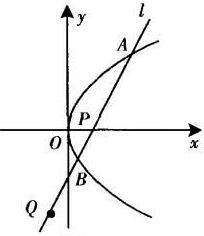如图，已知P为抛物线y2=4x的焦点，过点P的直线l与抛物线交于A，B两点，若点Q在直线AB上，且满足|