题目内容
关于x的方程ax2+ax+1=0有正根，求a的取值范围．
考点：一元二次方程的根的分布与系数的关系,根的存在性及根的个数判断
专题：函数的性质及应用
分析：关于x的方程ax2+ax+1=0有正根?（1）当方程有两个正根（2）当方程有一个正根一个负根（3）当方程有一个正根一个零根，结合二次方程的根的情况可求．
解答：
解：（1）当方程有两个正根时，
无解；
（2）当方程有一个正根一个负根时，
解得a＜0；
（3）当方程有一个正根一个零根时，
∵将0代入方程得1=0
∴不可能有0根，
总之，a的取值范围：a＜0．
|
（2）当方程有一个正根一个负根时，
|
（3）当方程有一个正根一个零根时，
∵将0代入方程得1=0
∴不可能有0根，
总之，a的取值范围：a＜0．
点评：本题考查一元二次方程根的分布与系数的关系，考查分类讨论的思想，是中档题．
练习册系列答案
相关题目
某市新年第一个月前10天监测到空气污染指数如表（主要污染物为可吸入颗粒物）：（第天监测得到的数据记为ai）已知函数f（x）是定义在R上的奇函数，若g（x）=f（x+1）+5，g（x）=f（x+1）+5，g′（x）为g（x）的导函数，对?x∈R，总有g′（x）＞2x，则g（x）＜x2+4的解集为（ ）
| A、（-∞，-1） |
| B、（-∞，1） |
| C、R |
| D、（-1，+∞） |
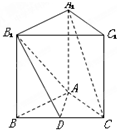如图，底面是正三角形的直三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=2．
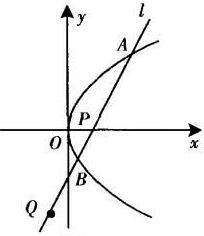如图，已知P为抛物线y2=4x的焦点，过点P的直线l与抛物线交于A，B两点，若点Q在直线AB上，且满足|