题目内容
设a,b∈R,关于x的方程(x2-ax+1)(x2-bx+1)=0的四个实根构成以q为公比的等比数列,若q∈[
,2],则ab的取值范围为 .
| 1 |
| 3 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:利用等比数列的性质确定方程的根,由韦达定理表示出ab,再利用换元法转化为二次函数,根据Q的范围和二次函数的性质,确定ab的最值即可求出ab的取值范围.
解答:
解:设方程(x2-ax+1)(x2-bx+1)=0的4个实数根依次为m,mq,mq2,mq3,
由等比数列性质,不妨设m,mq3为x2-ax+1=0的两个实数根,则mq,mq2为方程x2-bx+1=0的两个根,
由韦达定理得,m2q3=1,m+mq3=a,mq+mq2=b,则m2=
故ab=(m+mq3)(mq+mq2)=m2(1+q3)(q+q2)
=
(1+q3)(q+q2)=q+
+q2+
,
设t=q+
,则q2+
=t2-2,
因为q∈[
,2],且t=q+
在[
,1]上递减,在(1,2]上递增,
所以t∈[2,
],
则ab=t2+t-2=(t+
)2-
,
所以当t=2时,ab取到最小值是4,
当t=
时,ab取到最大值是
,
所以ab的取值范围是:[4,
].
由等比数列性质,不妨设m,mq3为x2-ax+1=0的两个实数根,则mq,mq2为方程x2-bx+1=0的两个根,
由韦达定理得,m2q3=1,m+mq3=a,mq+mq2=b,则m2=
| 1 |
| q3 |
故ab=(m+mq3)(mq+mq2)=m2(1+q3)(q+q2)
=
| 1 |
| q3 |
| 1 |
| q |
| 1 |
| q2 |
设t=q+
| 1 |
| q |
| 1 |
| q2 |
因为q∈[
| 1 |
| 3 |
| 1 |
| q |
| 1 |
| 3 |
所以t∈[2,
| 10 |
| 3 |
则ab=t2+t-2=(t+
| 1 |
| 2 |
| 9 |
| 4 |
所以当t=2时,ab取到最小值是4,
当t=
| 10 |
| 3 |
| 112 |
| 9 |
所以ab的取值范围是:[4,
| 112 |
| 9 |
点评:本题考查等比数列的性质,韦达定理,以及利用换元法转化为二次函数,考查学生分析解决问题的能力,正确转化是解题的关键.

练习册系列答案
相关题目
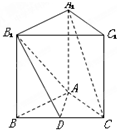 如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=2.
如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=2.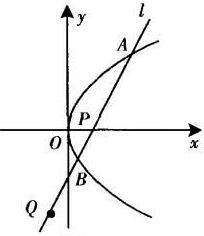 如图,已知P为抛物线y2=4x的焦点,过点P的直线l与抛物线交于A,B两点,若点Q在直线AB上,且满足|
如图,已知P为抛物线y2=4x的焦点,过点P的直线l与抛物线交于A,B两点,若点Q在直线AB上,且满足|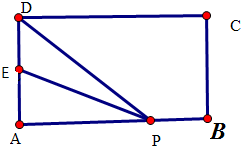 如图,在矩形ABCD中,E是AD的中点,P是AB边上的点,AB=3,AD=2
如图,在矩形ABCD中,E是AD的中点,P是AB边上的点,AB=3,AD=2