题目内容
已知数列{an}中,a1=2,an+1=an2+an-
(n∈N*)
(1)证明:数列{lg(an+
)是等比数列,并求数列{an}的通项公式;
(2)记数列{bn}满足bn=lg(an+
),求数列{bn}的前n项和Sn.
| 1 |
| 4 |
(1)证明:数列{lg(an+
| 1 |
| 2 |
(2)记数列{bn}满足bn=lg(an+
| 1 |
| 2 |
考点:数列的求和,等比数列的通项公式,等比关系的确定
专题:等差数列与等比数列
分析:(1)把已知的递推式变形,得到an+1+
=(an+
)2,两边取对数后得数列{lg(an+
)}是等比数列,求其通项公式后可得数列{an}的通项公式;
(2)直接利用等比数列的前n项和公式得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)直接利用等比数列的前n项和公式得答案.
解答:
证明:(1)由an+1=an2+an-
,得an+1+
=(an+
)2,
∴lg(an+1+
)=lg(an+
)2=2lg(an+
),
∴
=2.
则数列{lg(an+
)}是以lg(a1+
)=lg
为首项,以2为公比的等比数列,
∴lg(an+
)=(lg
)•2n-1,即an+
=(
)2n-1,
∴an=(
)2n-1-
;
(2)∵数列{lg(an+
)}是以lg(a1+
)=lg
为首项,以2为公比的等比数列,
∴Sn=n•lg
+
=lg(
)n+n2-n.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴lg(an+1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
lg(an+1+
| ||
lg(an+
|
则数列{lg(an+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴lg(an+
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴an=(
| 5 |
| 2 |
| 1 |
| 2 |
(2)∵数列{lg(an+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴Sn=n•lg
| 5 |
| 2 |
| 2n(n-1) |
| 2 |
| 5 |
| 2 |
点评:本题考查了等比关系的确定,考查了等比数列的通项公式与等比数列的前n项和,是中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
函数f(x)=x3+3x-1在以下哪个区间一定有零点( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
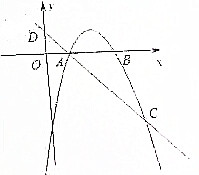 如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).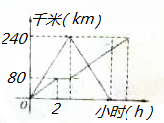 甲,乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,中途到达B地并在B地停留1小时后按原速驶向C地;同时乙车从C地出发匀速向A地行驶,到达A地后,立即按原路原速返回到C地并停留.在两车行驶的过程中,甲,乙两车距各自出发地的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,请结合图象回答下列问题:
甲,乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,中途到达B地并在B地停留1小时后按原速驶向C地;同时乙车从C地出发匀速向A地行驶,到达A地后,立即按原路原速返回到C地并停留.在两车行驶的过程中,甲,乙两车距各自出发地的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,请结合图象回答下列问题: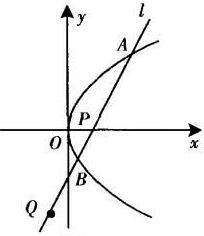 如图,已知P为抛物线y2=4x的焦点,过点P的直线l与抛物线交于A,B两点,若点Q在直线AB上,且满足|
如图,已知P为抛物线y2=4x的焦点,过点P的直线l与抛物线交于A,B两点,若点Q在直线AB上,且满足|