题目内容
将斜边为
的等腰直角三角形绕其一直角边所在直线旋转一周,所得几何体的侧面积是多少?
| 2 |
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:判断旋转体是圆锥,求出底面半径母线长,得出出底面周长,然后求出表面积.
解答:
解:等腰直角三角形的斜边边长为
,直角边为1,
则以一直角边所在的直线为轴旋转一周所成的几何体是圆锥,
底面半径为1,
圆锥的底面周长为:2π,母线长为:
,
圆锥的侧面积为:
×2π×
=
π,
故答案为:
π.
| 2 |
则以一直角边所在的直线为轴旋转一周所成的几何体是圆锥,
底面半径为1,
圆锥的底面周长为:2π,母线长为:
| 2 |
圆锥的侧面积为:
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查的知识点是圆锥的几何特征,当用一个直角三角形绕其一直角边旋转形成圆锥时,找到其底面半径的长和母线长是解答本题的关键

练习册系列答案
相关题目
从装有2个黄球和2个蓝球的口袋内任取2个球,则恰有一个黄球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点Q(0,3)及抛物线y2=16x上一动点P(x0,y0),则x0+|PQ|的最小值为( )
| A、1 | B、2 | C、4 | D、5 |
分别以直角三角形的斜边和两直角边所在直线为轴,将三角形旋转一周所得旋转体的体积依次为V1、V2、V3,则( )
| A、V1=V2+V3 | ||||||
| B、V12=V22+V32 | ||||||
C、
| ||||||
D、
|
函数f(x)=x2在下列哪个区间存在零点( )
| A、(-3,-1) |
| B、(-1,2) |
| C、(2,3) |
| D、(3,4) |
在△ABC中,c=
,A=75°,B=60°,则b等于( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
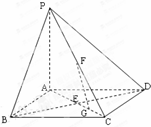 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.