题目内容
空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且PQ=2,QR=
,PR=3,那么异面直线AC和BD所成的角是 .
| 5 |
考点:异面直线及其所成的角
专题:空间角
分析:由于AB、BC、CD的中点分别是P、Q、R,利用三角形的中位线定理可得PQ∥AC,QR∥BD.因此∠PQR或其补角是异面直线AC和BD所成的角.再利用勾股定理的逆定理即可得出.
解答:
解:如图所示,∵AB、BC、CD的中点分别是P、Q、R,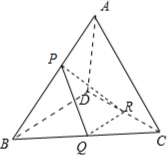
∴PQ∥AC,QR∥BD.
∴∠PQR或其补角是异面直线AC和BD所成的角.
∵PQ=2,QR=
,PR=3,∴PQ2+QR2=PR2.
∴PQ⊥QR.
∴∠PQR=90°.
∴异面直线AC和BD所成的角是90°.
故答案为:90°.

∴PQ∥AC,QR∥BD.
∴∠PQR或其补角是异面直线AC和BD所成的角.
∵PQ=2,QR=
| 5 |
∴PQ⊥QR.
∴∠PQR=90°.
∴异面直线AC和BD所成的角是90°.
故答案为:90°.
点评:本题考查了三角形的中位线定理、异面直线所成的角、勾股定理的逆定理,考查了推理能力,属于基础题.

练习册系列答案
相关题目
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的极坐标方程为θ=
(ρ∈R),它与圆
(α为参数)相切,则|a-b|= .
| π |
| 4 |
|
对两个变量x和y进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )
A、由样本数据得到的回归方程
| ||||||||||||
| B、残差平方和越小的模型,拟合的效果越好 | ||||||||||||
C、用相关指数R2=1-
| ||||||||||||
D、用相关指数R2=1-
|
设F1,F2是双曲线C的两焦点,点M在双曲线上,且∠MF2F1=
,若|F1F2|=8,|F2M|=
,则双曲线C的实轴长为( )
| π |
| 4 |
| 2 |
A、2
| ||
B、4
| ||
C、2
| ||
D、4
|
一个圆锥的正视图是边长为4的等边三角形,则这个圆锥的表面积为( )
| A、4π | B、8π |
| C、12π | D、16π |

