题目内容

已知椭圆
x2
25
+
y2
16
=1与双曲线
x2
8
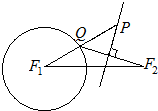
-y2=1有公共焦点F1，F2，P为椭圆与双曲线的一个交点，则面积SPF1F2为（　　）
A．3B．4C．5D．6
椭圆
x2
25
+
y2
16
=1与双曲线
x2
8
-y2=1的公共焦点为F1（3，0）、F2（-3，0）．
∴焦距|F1F2|=6．
设P（m，n）是椭圆与双曲线的一个交点，
则
m2
25
+
n2
16
=1
m2
8
-n2=1
，解之得
m2=
200
9
n2=
16
9
，得P（
10
2
3
，±
4
3
）或P（-
10
2
3
，±
4
3
）．
∴△PF1F2的面积S△PF1F2=
1
2
•|F1F2|•|n|=
1
2
×6×
4
3
=4．
故选：B
练习册系列答案
相关题目
双曲线两条渐近线互相垂直，那么它的离心率为（　　）
A．
2
B．
3
C．2D．
3
2
若方程
x2
k+2
+
y2
5-k
=-1表示双曲线，则k的取值范围是______．
如图，点F2是⊙F1外的一点，点Q是⊙F1上的动点，射线F1Q交线段F2Q的中垂线于P，则点P一定在（　　）
A．以F1、F2为焦点，以2|F1Q|为长轴长的椭圆上
B．以F1、F2为焦点，以2|F1Q|为实轴长的双曲线上
C．以F2为焦点，以F1F2中点为顶点的抛物线上
D．以F1、F2为焦点，以|F1Q|为实轴长的双曲线上
设F1，F2是双曲线x2-
y2
4
=1的左、右两个焦点，若双曲线右支上存在一点P，使（
OP
+
OF2
）•
F2P
=0（O为坐标原点），且|PF1|=λ|PF2|，则λ的值为______．
双曲线
x2
4
-
y2
9
=-1的渐近线方程是（　　）
A．y=
+-
2
3
x		B．y=
+-
4
9
x		C．y=
+-
3
2
x		D．y=
+-
9
4
x
如果圆锥曲线
y2
λ+5
-
x2
2-λ
=1的焦距与实数λ无关，那么它的焦点坐标是______．
点P在双曲线x2-y2=1上运动，O为坐标原点，线段PO中点M的轨迹方程是______．
已知双曲线C1与抛物线C2：y2＝8x有相同的焦点F，它们在第一象限内的交点为M，若双曲线C1的焦距为实轴长的2倍，则|MF|＝________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网