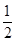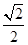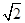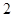题目内容
设F1,F2是双曲线x2-
=1的左、右两个焦点,若双曲线右支上存在一点P,使(
+
)•
=0(O为坐标原点),且|PF1|=λ|PF2|,则λ的值为______.
| y2 |
| 4 |
| OP |
| OF2 |
| F2P |
由双曲线方程x2-
=1可得
a=1,b=2,c=
,
∴|
|=
又∵(
+
)•
=0
∴(
+
)•(
-
)=0
∴
2-
2=0
∴|
|=|
|=
故△PF1F2是以P为直角的直角三角形
又∵P是双曲线右支上的点
∴|PF1|>|PF2|,
∴|PF1|=|PF2|+2,
由勾股定理可得|PF1|2+(|PF2|+2)2=4C2=20
解得|PF2|=2,|PF1|=4
故λ=2
故答案为2
| y2 |
| 4 |
a=1,b=2,c=
| 5 |
∴|
| OF2 |
| 5 |
又∵(
| OP |
| OF2 |
| F2P |
∴(
| OP |
| OF2 |
| OP |
| OF2 |
∴
| OP |
| OF2 |
∴|
| OP |
| OF2 |
| 5 |
故△PF1F2是以P为直角的直角三角形
又∵P是双曲线右支上的点
∴|PF1|>|PF2|,
∴|PF1|=|PF2|+2,
由勾股定理可得|PF1|2+(|PF2|+2)2=4C2=20
解得|PF2|=2,|PF1|=4
故λ=2
故答案为2

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
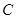 :
: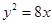 与点
与点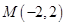 ,过
,过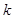 的直线与
的直线与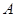 ,
,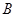 两点,若
两点,若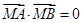 ,则
,则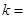 ( )
( )