题目内容
已知圆x2+y2-4x-4=0上的点P(x,y),则x2+y2的最大值为 .
考点:圆的一般方程,两点间距离公式的应用
专题:直线与圆
分析:利用圆的参数方程求解.
解答:
解:∵圆x2+y2-4x-4=0上的点P(x,y),
∴圆心(2,0),半径r=
=2
,
∴
,0≤θ<2π,
∴x2+y2=(2+2
cosθ)2+(2
sinθ)2=8sin2θ+8cos2θ+8
cosθ+4
=12+8
cosθ,
∴x2+y2的最大值为12+8
.
故答案为:12+8
.
∴圆心(2,0),半径r=
| 1 |
| 2 |
| 16+16 |
| 2 |
∴
|
∴x2+y2=(2+2
| 2 |
| 2 |
| 2 |
=12+8
| 2 |
∴x2+y2的最大值为12+8
| 2 |
故答案为:12+8
| 2 |
点评:本题考查代数和的最大值的求法,是基础题,解题时要注意圆的参数方程和三角函数的性质的合理运用.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若m∥n,n?α则 m∥α |
| B、若m?α,α⊥β,则m⊥β |
| C、若m∥n,m⊥α,则n⊥α |
| D、若m⊥n,m?α,n?β,则α⊥β |
若f(x)=-
x2+(a+2)x+lnx在(1,+∞)上是减函数,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,-2] |
| B、(-3,-1) |
| C、[-1,0) |
| D、[0,+∞) |
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<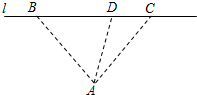 某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=
某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=