题目内容
19.已知$α∈(\frac{π}{2},π)$,且$sinα=\frac{4}{5}$,则tanα=( )| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
分析 根据同角的三角函数关系,进行计算即可.
解答 解:$α∈(\frac{π}{2},π)$,且$sinα=\frac{4}{5}$,
∴cosα<0
cosα=-$\sqrt{1{-sin}^{2}α}$=-$\sqrt{1{-(\frac{4}{5})}^{2}}$=-$\frac{3}{5}$
∴tanα=$\frac{sinα}{cosα}$=-$\frac{4}{3}$.
故选:D.
点评 本题考查了同角的三角函数关系应用问题,是基础题.

练习册系列答案
相关题目
7.已知函数f(x)=ln3x+ax+1(a∈R)的图象在点($\frac{1}{3}$,f($\frac{1}{3}$))处的切线的倾斜角是$\frac{3π}{4}$,则a=( )
| A. | -4 | B. | 4 | C. | 3 | D. | -3 |
4.设函数f(x)(x∈R)满足f(2-x)=f(x),且当x≥1时,f(x)=lnx,则有( )
| A. | f($\frac{1}{2}$)<f($\frac{1}{3}$)<f(2) | B. | f(2)<f($\frac{1}{2}$)<f($\frac{1}{3}$) | C. | f($\frac{1}{3}$)<f($\frac{1}{2}$)<f(2) | D. | f($\frac{1}{2}$)<f(2)<f($\frac{1}{3}$) |
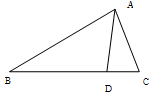 如图,在△ABC中,∠B=$\frac{π}{6}$,AB=8$\sqrt{3}$,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.
如图,在△ABC中,∠B=$\frac{π}{6}$,AB=8$\sqrt{3}$,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.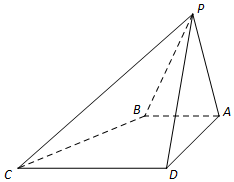 如图四棱锥P-ABCD中,侧面PAD⊥底面ABCD.△PAD是正三角形,四边形ABCD是直角梯形,AB∥CD,AD=CD=2AB,点E为PD中点.
如图四棱锥P-ABCD中,侧面PAD⊥底面ABCD.△PAD是正三角形,四边形ABCD是直角梯形,AB∥CD,AD=CD=2AB,点E为PD中点.