题目内容

6．在△ABC中，已知a=3，b=4，c=$\sqrt{37}$，则△ABC的面积是3$\sqrt{3}$．

分析 根据余弦定理求出cosC，根据同角三角函数的关系得出sinC，则S=$\frac{1}{2}absinC$．

解答 解：由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$，
∴sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{3}}{2}$．
∴S△ABC=$\frac{1}{2}absinC$=$\frac{1}{2}×3×4×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$．
故答案为3$\sqrt{3}$．

点评 本题考查了余弦定理，三角形的面积公式，属于基础题．

练习册系列答案
相关题目
16．已知f（x）为R上的奇函数，当x＞0时，f（x）=3x，那么f（-2）的值为-9．
17．若函数y=f（x）x∈[0，1]同时满足下列三个条件：①对任意的x∈[0，1]，总有f（x）≥0；②f（1）=1；③任意x1，x2∈[0，1]，当x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立，我们就称f（x）为“稳定函数”．请根据上述信息解决以下问题：
（1）已知h（x）是稳定函数，求h（0）的值；
（2）若函数g（x）=ax-1（a＞0且a≠1），问是否存在实数a，使得g（x）是稳定函数？请说明理由；
（3）已知f（x）是稳定函数，存在x0∈[0，1]，使得f（x0）∈[0，1]且f（f（x0））=x0，求证：f（x0）=x0．
14．平面直角坐标系中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的两点M，N，点P（2，1）为线段MN的中点，椭圆的离心率为$\frac{\sqrt{2}}{2}$．
（1）求直线MN的方程；
（2）若F1是椭圆C右焦点，且$\overrightarrow{{F}_{1}M}$•$\overrightarrow{{F}_{1}N}$=-$\frac{1}{3}$，求椭圆C的方程．
1．如图，该程序运行后输出的结果为（　　）
A．7B．11C．25D．36
11．将函数y=sin（ωx+φ）（ω＞0，0＜φ＜$\frac{π}{2}$）的图象向右平移$\frac{π}{6}$个单位后，得到函数y=cos（$\frac{π}{2}$-2x）的图象，则函数y=sin（ωx+φ）的对称中心是（$\frac{kπ}{2}$-$\frac{π}{6}$，0），k∈Z．
18．若$\overrightarrow{a}$=（2，3，m），$\overrightarrow{b}$=（2n，6，8）且$\overrightarrow{a}$，$\overrightarrow{b}$为共线向量，则m+n的值为（　　）
A．7B．$\frac{5}{2}$C．6D．8
15．一个几何体的三视图如图，则该几何体的体积为（　　）
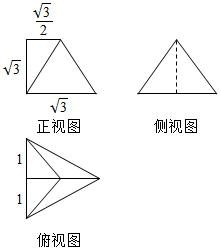
A．$\frac{1}{2}$B．1C．$\frac{3}{2}$D．2
16．设△ABC内角A，B，C的对边分别为a，b，c，已知bc=60，S△ABC=15$\sqrt{3}$．则A为（　　）
A．30°B．60°C．60°或120°D．30°或150°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网