题目内容
18.某高中有甲乙两个班级进行数学考试,按照大于或等于90分为优秀,90分以下为非优秀统计成绩后,得到如下的列联表:| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 55 |
| 合计 | 30 | 75 | 105 |
(2)根据列联表的数据,能否在犯错误的概率不超过0.05的前提下认为成绩与班级有关系?
参考公式:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}(其中n=a+b+c+d$为样本容量)
随机变量K2的概率分布:
| p(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据列联表各数据之间的关系求出未知空的数据;
(2)根据公式计算相关指数K2的观测值,比较临界值的大小,可判断成绩与班级有关系的可靠性程度.
解答 解:(1)列联表如下:
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
根据列联表中的数据,得到K2=$\frac{105×(10×30-20×45)^{2}}{55×50×30×75}$≈6.109>3.841,
因此有95%的把握认为“成绩与班级有关系”.
点评 本题考查了列联表及利用列联表进行独立性检验的思想方法,熟练掌握独立性检验的思想方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知三棱锥S-ABC,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC=3,则该三棱锥外接球的表面积为( )
| A. | 4$\sqrt{3}$π | B. | $\frac{27\sqrt{3}π}{2}$ | C. | 27π | D. | 9π |
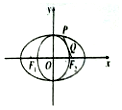 如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$.
如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$. 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.