题目内容
12.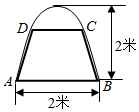 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.(Ⅰ)请建立适当的直角坐标系,求抛物线形钢板所在抛物线方程;
(Ⅱ)记CD=2x,写出梯形面积S以x为自变量的函数关系式,并指出定义域;
(Ⅲ)求面积S的最大值.
分析 (I)以抛物线定点为原点建立坐标系,使用待定系数法求出解析式;
(II)设梯形高为h,用x,h表示出C点坐标,代入解析式得出x,h的关系,代入梯形面积公式即可;
(III)利用导数判断S(x)的单调性,根据单调性得出最值.
解答  解:(I)如图,建立直角坐标系xoy,使抛物线的顶点在坐标原点,且抛物线的对称轴在y轴上.
解:(I)如图,建立直角坐标系xoy,使抛物线的顶点在坐标原点,且抛物线的对称轴在y轴上.
则A(-1,-2 ),B(1,-2),
设抛物线的标准方程为:x2=2py(p<0).
∵点B在抛物线上,∴12=2p•(-2)求得p=-$\frac{1}{4}$,
∴抛物线的方程为:${x^2}=-\frac{1}{2}y$.
(II)设梯形的高为 h,∵CD=2 x 则 C(x,-2+h ).
又点C在抛物线上,∴${x^2}=-\frac{1}{2}(-2+h)$,解得 h=-2x2+2.
∴S(x)=$\frac{1}{2}(2+2x)(-2{x^2}+2)$=2(-x3-x2+x+1).
定义域为(0,1).
(III)∵S(x)=2(-x3-x2+x+1).
∴S′(x)=2(-3x2-2x+1)=-2(3x-1)(x+1).
令S′(x)=0,解得x=-1(舍)或x=$\frac{1}{3}$.
当0$<x<\frac{1}{3}$时,S′(x)>0,当$\frac{1}{3}<x<1$时,S′(x)<0,
∴S(x)在$(0,\frac{1}{3})$上为增函数,$(\frac{1}{3},1)$上为减函数,
∴当x=$\frac{1}{3}$时,面积S取得最大值$S{(\frac{1}{3})_{max}}$=$\frac{64}{27}$.
答:梯形的面积S的最大值为$\frac{64}{27}$.
点评 本题考查了待定系数法求曲线方程,导数与函数的最值,属于中档题.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | $2\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 2 |
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
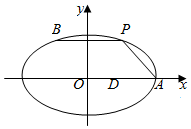 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$. 如图,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,O是坐标原点,|OF|=$\sqrt{5}$,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$.
如图,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,O是坐标原点,|OF|=$\sqrt{5}$,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为$\frac{4\sqrt{5}}{3}$. 在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.
在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.