题目内容
已知动圆C过定点M(0,2),且在x轴上截得弦长为4.设该动圆圆心的轨迹为曲线C.
(1)求曲线C的方程;
(2)设点A为直线l:x-y-2=0上任意一点,过A作曲线C的切线,切点分别为P,Q,求△APQ面积的最小值及此时点A的坐标.
解:(1)设动圆圆心坐标为C(x,y),根据题意,得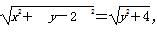
化简得x2=4y.
故曲线C的方程为x2=4y.
(2)设直线PQ的方程为y=kx+b,
由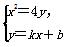 消去y,得x2-4kx-4b=0.
消去y,得x2-4kx-4b=0.
设P(x1,y1),Q(x2,y2),
则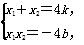 且Δ=16k2+16b.
且Δ=16k2+16b.
以点P为切点的切线的斜率为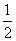 x1,其切线方程为y-y1=
x1,其切线方程为y-y1=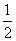 x1(x-x1),
x1(x-x1),
即y=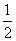 x1x-
x1x-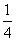 x
x ,
,
同理过点Q的切线的方程为y=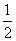 x2x-
x2x-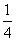 x
x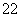 .
.
设两条切线的交点A(xA,yA),
∵x1≠x2,解得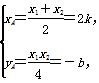
即A(2k,-b),
则2k+b-2=0,即b=2-2k,代入Δ=16k2+16b=16k2+32-32k=16(k-1)2+16>0,
∴|PQ|=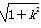 |x1-x2|
|x1-x2|
=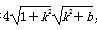
又A(2k,-b)到直线PQ的距离为d=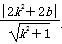 ,
,
∴S△APQ=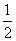 |PQ|·d=4|k2+b|·
|PQ|·d=4|k2+b|· =4(k2+b)
=4(k2+b) 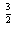 =4(k2-2k+2)
=4(k2-2k+2) 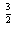 =4[(k-1)2+1]
=4[(k-1)2+1] 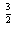 ,
,
∴当k=1时,S△APQ最小,其最小值为4,此时点A的坐标为(2,0).

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
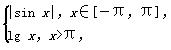
 的前n项和为Sn,若S2n+1-Sn≤
的前n项和为Sn,若S2n+1-Sn≤ 对n∈N*恒成立,则正整数m的最小值是________.
对n∈N*恒成立,则正整数m的最小值是________.
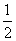 B.
B.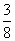 C.
C.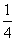 D.
D.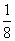
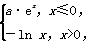
 x2-ln x-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是________.
x2-ln x-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是________.