题目内容
已知命题p:“∀x∈[1,2], x2-ln x-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是________.
x2-ln x-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是________.
(-∞,-4]∪
[解析] 命题p:a≤ x2-ln x在x∈[1,2]上恒成立,令f(x)=
x2-ln x在x∈[1,2]上恒成立,令f(x)= x2-ln x,
x2-ln x,
f′(x)=x-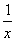 =
= ,当1<x<2时,f′(x)>0,
,当1<x<2时,f′(x)>0,
∴f(x)min=f(1)= .∴a≤
.∴a≤ .
.
命题q:Δ=4a2-4(-8-6a)≥0,∴a≥-2或a≤-4.
综上,两个命题都是真命题,则有a∈(-∞,-4]∪ .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
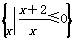 ,则集合∁UA等于( )
,则集合∁UA等于( )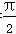 +kπ,y≠
+kπ,y≠


 )中加上一块糖(质量为
)中加上一块糖(质量为 )会变得更甜。这一事实可以抽象为一个数学问题:___________
)会变得更甜。这一事实可以抽象为一个数学问题:___________ ,则满足
,则满足 的
的 的值为____________
的值为____________