题目内容
已知函数f（x）=
，其中e是自然对数的底数，若直线y=2与函数y=f（x）的图象有三个交点，则常数a的取值范围是（ ）
|
| A、（-∞，2） |
| B、（-∞，2] |
| C、（2e-2，+∞） |
| D、[2e-2，+∞） |
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：由题意，二次函数开口应该向上，并且ae2≥2，得到a≥2e-2，得到选项．
解答：
解：函数图象如下，
要使直线y=2与函数y=f（x）的图象有三个交点，只要ae2≥2，解得a≥2e-2；
故选D．
要使直线y=2与函数y=f（x）的图象有三个交点，只要ae2≥2，解得a≥2e-2；
故选D．
点评：本题考查了数形结合解决函数图象的交点个数问题，属于经常考查内容．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
，
满足|
|=1，|
|=2，且（
+
）⊥
，则向量
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
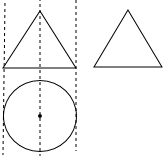如图，一个空间几何体的正视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么这个几何体的内切球表面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|