题目内容
已知函数f(x)=-x3+ax2+1(a∈R).
(1)函数y=f(x)是否可能在R上是单调函数?若可能,求出实数a的取值范围.
(2)若函数y=f(x)在区间(0,
)上递增,在区间(1,+∞)上递减,求出实数a的取值范围.
(1)函数y=f(x)是否可能在R上是单调函数?若可能,求出实数a的取值范围.
(2)若函数y=f(x)在区间(0,
| 2 |
| 3 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)由f(x)的解析式求出导函数,导函数为开口向下的抛物线,若函数在R上为单调增函数,所以导函数对应方程的判别式△≤0,列出关于a的不等式,求出不等式的解集即可得到实数a的取值范围,(2)求导令f'(x)=0,依题意对导函数符号做出分析.
解答:
解:(1)∵f′(x)=-3x2+2ax,
若f(x)在R上单调,只需△≤0,即4a2+12≤0即a=0,
此时f′(x)≤0,f(x)在R上递减;
(2)由于函数f(x)=-x3+ax2+1(a∈R),
则导函数f′(x)=-3x2+2ax=x(-3x+2a),
则f'(x)=0 有两根x1=0 x2=
,
又函数y=f(x)在区间(0,
)上递增,在区间(1,+∞)上递减,
则要求在区间(0,
)上,导函数f′(x)≥0;
且在区间(1,+∞)上,导函数f′(x)≤0,
所以
≤x2≤1,即
≤
≤1,
解得1≤a≤
.
若f(x)在R上单调,只需△≤0,即4a2+12≤0即a=0,
此时f′(x)≤0,f(x)在R上递减;
(2)由于函数f(x)=-x3+ax2+1(a∈R),
则导函数f′(x)=-3x2+2ax=x(-3x+2a),
则f'(x)=0 有两根x1=0 x2=
| 2a |
| 3 |
又函数y=f(x)在区间(0,
| 2 |
| 3 |
则要求在区间(0,
| 2 |
| 3 |
且在区间(1,+∞)上,导函数f′(x)≤0,
所以
| 2 |
| 3 |
| 2 |
| 3 |
| 2a |
| 3 |
解得1≤a≤
| 3 |
| 2 |
点评:本题主要考查了利用导数研究函数的单调性,以及恒成立问题的转化,掌握二次函数恒成立时所取的条件,属于综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
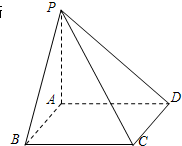 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
已知函数f(x)=
,其中e是自然对数的底数,若直线y=2与函数y=f(x)的图象有三个交点,则常数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,2] |
| C、(2e-2,+∞) |
| D、[2e-2,+∞) |
若椭圆
+
=1的一个焦点和短轴的两端点构成一个正三角形,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|